Дипломная работа: Полуполя, являющиеся простыми расширениями с помощью комплексного числа

То есть, дискриминант D_{l +1} имеет тот же знак, что и D_l . Так как D ₀ <0, то пользуясь методом математической индукции заключаем, что любой дискриминант D_l <0.

Рассмотрим неравенство , подставим , . Получим

.

То есть,

.

Зная, что заметим

.

Итак, для доказательства нам достаточно установить, что

.

То есть,

.

Пусть аналогичными рассуждениями мы установили, что нам достаточно доказать неравенство

.

Тогда

.

Раскрывая скобки и приводя подобные слагаемые, получим, что

.

Используя оценку и деля на положительный элемент , получаем

.

Обозначим . Рассмотрим отображение , заданное по правилу . При , . Отображение является сжимающим. Оно имеет единственную неподвижную точку. Найдем ее: . Откуда . Заметим, что . Последовательность стремится к 4. То есть, нам достаточно установить, что , а это следует из (*). Итак, мы доказали, что . То есть, мы нашли такой многочлен, , что . Итак, мы доказали, что если удовлетворяет минимальному соотношению, являющемуся квадратным уравнением без положительных корней, то – поле. ■

Следствие 1. Если – мнимый корень квадратного трехчлена, то ‑ поле.

Следствие 2. Любое простое расширение является полем , порожденным минимальным соотношением 2 степени.

Доказательство.

Заметим, что . Покажем, что для любого a ÎQ найдется такой квадратный многочлен , что - его корень многочлена. Для этого достаточно представить . Возьмем такой , что , тогда . Очевидно, . Таким образом, нам удалось найти многочлен из . То есть, - поле. ■

Рассмотрим последовательность действительных чисел :

(**)

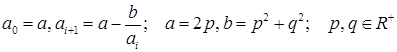Будем говорить, что последовательность задается числами p и q .

Лемма 2.3.3. Существует n , что .

Доказательство. Пусть . Покажем, что последовательность убывающая.

,

то есть .

Пусть , тогда

Так как , то

Пользуясь методом математической индукции, заключаем, что , то есть - убывающая.

Так как - монотонно убывающая и ограничена снизу 0, то существует . Тогда .

То есть, . Но тогда

,

,

что невозможно для . То есть, . ■

Лемма 2.3.4. Если , то существует , что .

Доказательство. Запишем а и bв виде десятичных дробей: