Тогда . Рассмотрим число .

То есть, . ■

Теорема 2.3.5. Если и , то

.

Доказательство. По лемме 2.3.3, . Пусть .

Если n=1, то . Рассмотрим .

То есть,

.

Так как . По лемме 2.3.4 . Тогда

.

Рассмотрим n > 1.

Пусть .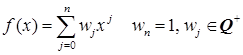

Покажем, что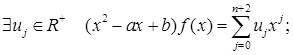

Раскроем скобки и сгруппируем члены при x^j .

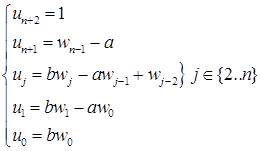
То есть,

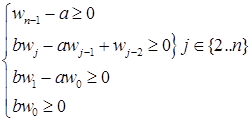
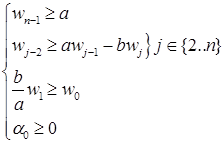
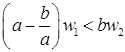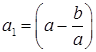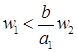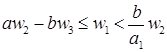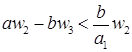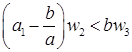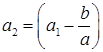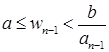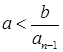Заметим, что . Для существования , по лемме 2.3.4, достаточно выполнения условий и , то есть, . Обозначим . Так как , то и . Для существования достаточно доказать существование и . То есть, . Обозначим . Повторим эту операцию n-2 раза. Получим, что . По лемме 2.3.4, существует, если и 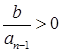. Эти условия следуют из того, что 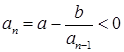и .

Таким образом, доказано существование

■

Теорема 2.3.6. Если минимальный многочлен f - g порождает полуполе то, он либо имеет положительный действительный корень, либо корень , такой что и последовательность (**), заданная числами p и q , не содержит отрицательных элементов.

Доказательство. Пусть многочлен f - g не имеет положительных действительных корней, и для всех корней вида , где , последовательность (**), заданная числамиp и q , содержит отрицательный элемент. Тогда, по теореме 2.3.5, для каждого множителя вида существует многочлен , что . Рассмотрим многочлен . так как и . Кроме того , а остальные множители многочлена имеют вид или . То есть, . Таким образом . По теореме 2.1.1, минимальный многочлен порождает поле. ■

Теорема 2.3.7. Для комплексных чисел расширение , минимальное соотношение которого имеет положительный корень, является полуполем.

Доказательство. Пусть a ' – положительный корень минимального соотношения. Предположим, что – поле. Тогда существует многочлен f с положительными коэффициентами, делящийся на минимальный многочлен. Значит f (a ' )=0. Но . Значит a ' – не является корнем многочлена f . То есть – полуполе. ■

2.4. Примеры

1. Рассмотрим . Оно удовлетворяет минимальному соотношению . По теореме 2.3.7, - полуполе. Аналогично доказывается, что – полуполе.

2. – полуполе. Для доказательства нужно воспользоваться теоремой 2.3.1.

3. Покажем, что – полуполе. Во-первых, заметим, что . Рассмотрим . По теореме 2.3.7, ‑ полуполе. Тогда, по теореме 2.3.1, – полуполе. . То есть, – полуполе.

4. , минимальное соотношение которого имеет вид , есть полуполе. Действительно, многочлен имеет положительный корень, а значит - полуполе.

Теперь приведем примеры полей.

5. является полем, потому что его минимальный многочлен имеет вид .

6. Пусть удовлетворяет минимальному соотношению . Его минимальный многочлен делит . То есть, – поле. Несложно видеть, что . Итак, .

7. Пусть удовлетворяет минимальному соотношению . Тогда – поле.

8. Пусть , если , то – поле. Так как , то Если , то . Рассмотрим последовательность (**), порожденную p и q . . По теореме 2.3.7, – поле.

Литература

1. Вечтомов Е.М. Введение в полукольца. – Киров: Изд-во Вятского гос. пед. ун-та, 2000