Математика / Дипломная работа: Полуполя, являющиеся простыми расширениями с помощью комплексного числа

Дипломная работа: Полуполя, являющиеся простыми расширениями с помощью комплексного числа

(3) ;

(4) ;

(5) .

Доказательство. Несложно установить равносильность утверждений (1) ‑ (4), исходя из предыдущей теоремы. Докажем условие равносильность их утверждению (5).

Из условия (5) следует, что никакой элемент не обратим по сложению. Тогда Q ⁺ (a ) не является полем, а значит Q ⁺ (a ) – полуполе. Докажем, что из (3) следует (5). Действительно, согласно условию (3),

("h Î Q ⁺ [a ],h ≠0) h (a )≠0.

То есть, если h (a )=0, то h =0. Пустьh (a )=(x +y )(a )=0. Тогда

Тогда (x_i +y_i )=0.

Так как x_i ÎQ ⁺ и y_i ÎQ ⁺ , то x_i = y_i =0. А значит, x = y =0.

Теорема доказана.

■

2.2. Расширения полуполя неотрицательных действительных чисел комплексным числом

Теорема 2.2.1. Любое расширение , где , является полем С .

Доказательство. Пусть , и при a > 0. Тогда находится строго в первой или четвертой четверти комплексной плоскости.

Очевидно, существует натуральное n , что лежит строго во второй или третьей четверти. То есть, , где c < 0, . Значит, и . По теореме 2.1.1, – поле. Очевидно, что . То есть, является полем С .

Аналогично рассматривается случай ■

2.3. Расширения полуполя неотрицательных рациональных чисел комплексным числом

Теорема 2.3.1. Если , то – поле тогда и только тогда, когда Q ⁺ (- a ² ) – поле.

Доказательство. По теореме 2.1.1 Q ⁺ (ai ) – поле равносильно существованию

f ¹0, f (ai )=0.

Так как все степени ai Î Q ⁺ (ai ). Рассмотрим некоторый многочлен

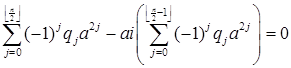Равенство выполняется тогда и только тогда, когда действительная и мнимая часть равны нулю.

То есть,

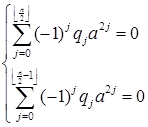
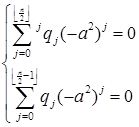
Это верно тогда и только тогда, когда Q ⁺ (-a ² ) – поле.

Получили, чтоQ ⁺ (ai ) – поле тогда и только тогда, когдаQ ⁺ (- a ² ) – поле. ■

Как следствие получаем более ценные утверждения.

Следствие 1. Если , то Q ⁺ ( ai ) – полуполе тогда и только тогда, когда Q ⁺ (- a ² ) – полуполе.

Следствие 2 . Если и Q ⁺ (- b ² ) – полуполе, a Î Q ⁺ (- b ² ), то Q ⁺ ( a + bi ) – полуполе.

Теорема 2.3.2. Пусть – комплексный корень квадратного трехчлена f ( x ) неприводимого над Q . Тогда – полуполе в том и только том случае, когда f ( x ) имеет положительный действительный корень.

Доказательство. Пусть удовлетворяет минимальному соотношению, являющемуся квадратным уравнением без положительных корней. Тогда , где D – дискриминант минимального соотношения.

Рассмотрим минимальный многочлен, соответствующий данному минимальному значению. Он имеет вид . Если b , c ≥ 0, то имеем многочлен из . Пусть многочлен имеет два отрицательных корня, тогда , . То есть . Если многочлен не имеет действительных корней, то