Математика / Дипломная работа: Полуполя, являющиеся простыми расширениями с помощью комплексного числа

Дипломная работа: Полуполя, являющиеся простыми расширениями с помощью комплексного числа

Определение: Алгебра <P, +, ×> называется полуполем , если

(1) <Р, +> – коммутативная полугруппа с 0;

(2) <Р, ×> – группа с 1;

(3) Дистрибутивность

(4)

Не сложно показать, что Q ⁺ является полуполем.

Определение: Пусть Р – подполуполе полуполя F , , тогда простым расширением полуполя P с помощью элемента a называется наименьшее подполуполе полуполя F , содержащее множество P и элемент a . Простое расширение P с помощью a обозначается P (a ).

1.2. Простое расширение Q ⁺ (a )

Теорема 1.2.1. Произвольное полутело либо аддитивно идемпотентно, либо содержит копию Q ⁺ в качестве полутела.

Доказательство. Предположим, что S – неидемпотентное полутело, т.е. найдется такой ненулевой элемент s ÎS , что s +s ¹s . Откуда

Рассмотрим суммы единиц. Через обозначим сумму k единиц (при k ÎN ). Так как любое полутело является антикольцом, то . Покажем, что суммы различного числа единиц в S различны. Допустим от противного, что при некоторых натуральных m <n . Положим l = n - m ÎN . Тогда . Прибавляя к обеим частям этого равенства элемент , получим

Применяя эту процедуру несколько раз, будем иметь

для любого t ÎN .

По свойству Архимеда, найдется такое t ÎN , что tl >n. При k= tl имеем и n< k . Тогда

Откуда 1=1+1 (). Получили противоречие.

Следовательно, полутело S содержит аддитивную копию N . Но тогда S содержит и частные сумм 1, т.е. содержит копию полуполя Q ⁺ , причем, очевидно, операции в Q ⁺ и S согласованы.

■

Теорема 1.2.2. 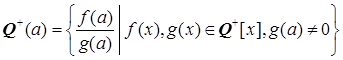- простое расширение полуполя Q ⁺ .

Доказательство. Заметим, что Q ⁺ (a ) – полуполе. Кроме того, а Î Q ⁺ (a ). Это не сложно увидеть, взяв . Очевидно .

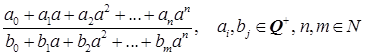Предположим, что есть полуполе P меньшееQ ⁺ (a ), содержащее а и Q ⁺ . Тогда оно содержит все выражения вида . Так как P – полуполе, то . Таким образом, . Так как P – минимальное полуполе, то . То есть, –простое расширение полуполя Q ⁺ .

■

Аналогично доказывается следующее утверждение.

Теорема 1.2.3. 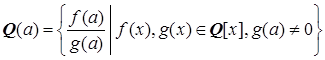- простое расширение поля Q .

1.3. Минимальное соотношение алгебраического элемента над полуполем рациональных неотрицательных чисел

Пусть а – алгебраическое число. Тогда минимальный многочлен F числа а имеет степень ≥ 1. Тогда обозначим через f многочлен, составленный из положительных одночленов многочлена F , а многочлен g составим из отрицательных членов, взятых с противоположными знаками. Тогда . , тогда .

Покажем, что любое равенство получается из , где . Заметим, что , так как а – корень , а – минимальный многочлен для a . Представим , где составлен из положительных одночленов многочлена h , а ‑ составлен из отрицательных одночленов многочлена h , взятых с противоположным знаком. Таким образом,