Дипломная работа: Разработка программного обеспечения для голосового управления трехмерными моделями функционирования промышленных роботов

(1.38)

или через модуль и фазу

(1.39)

Инвариантная к сдвигу линейная система называется физически реализуемой, если h (n )=0 при n <0. Линейная система устойчива, если для любой ограниченной по уровню входной последовательности выходная последовательность также ограничена. Необходимым и достаточным условием устойчивости линейной системы с постоянными параметрами является

(1.40)

Это условие аналогично (1.10) и оказывается достаточным для существования .

Сигналы на входе и выходе линейных инвариантных к сдвигу систем, таких, например, как фильтры, связаны дискретной сверткой (1.5) и кроме того, разностным уравнением

(1.41)

Вычисляя z -преобразование от обеих частей, можно получить

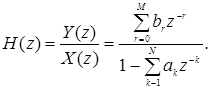(1.42)

Сравнивая (1.41) и (1.42), полезно отметить следующее. Если задано разностное уравнение вида (1.41), то H(z)можно получить непосредственной подстановкой коэффициентов при входном сигнале в числитель передаточной функции к соответствующим степеням z^-1 , а коэффициенты при выходном сигнале - в знаменатель к соответствующим степеням z^-1 .

Передаточная функция в общем случае является дробно рациональной. Таким образом, она определяется положением нулей и полюсов на z-плоскости. Это означает, что H(z)можно представить в виде

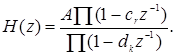(1.43)

При рассмотрении z -преобразования отмечалось, что физически реализуемые системы имеют область сходимости вида |z| >R ₁ . Если система, кроме того, еще и устойчива, то R ₁ должно быть меньше единицы, таким образом единичная окружность входит в область сходимости. Иначе говоря, для устойчивой системы все полюсы H(z) должны лежать внутри единичной окружности.

Достаточно определить два типа линейных систем с постоянными параметрами. Это системы с конечной импульсной характеристикой (КИХ) и системы с бесконечной импульсной характеристикой (БИХ). Эти два класса обладают отличными друг от друга свойствами, которые будут рассмотрены ниже.

Если все коэффициенты а_k . в уравнении (1.22) равны нулю, то разностное уравнение принимает вид

(1.44)

Сравнивая (1.44) с (1.56), можно отметить, что

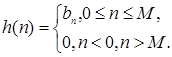(1.45)

Системы с КИХ обладают рядом важных свойств. Передаточная функция H(z) таких систем представляет собой полином по степеням z^-1 и, таким образом, не имеет ненулевых полюсов, а содержит только нули. Системы с КИХ могут обладать строго линейной фазо-частотной характеристикой (ФЧХ). Если h (n ) удовлетворяет условию

(1.46)

то

(1.47)

где - действительная или чисто мнимая величина в зависимости от знака в (1.48).

Возможность получения строго линейной ФЧХ является очень важным обстоятельством применительно к речевым сигналам в тех случаях, когда требуется сохранить взаимное расположение элементов сигнала. Это свойство систем с КИХ существенно облегчает решение задачи их проектирования, поскольку все внимание можно уделять лишь аппроксимации амплитудно-частотной характеристики (АЧХ). За это достоинство фильтра с линейной ФЧХ, приходится расплачиваться необходимостью аппроксимации протяженной импульсной реакции в случае фильтров с крутыми АЧХ. Хорошо разработаны три метода проектирования КИХ-фильтров с линейными ФЧХ: взвешивания, частотной выборки и проектирования оптимальных фильтров с минимаксной ошибкой [1-3]. Второй и третий методы являются оптимизационными и используют итеративный (в отличие от замкнутой формы) подход для определения коэффициентов фильтра. Несмотря на простоту метода взвешивания, широкое применение нашли все три метода. Это обусловлено завершенностью глубоких исследований оптимальных КИХ-фильтров а, кроме того, наличием подробно описанных программ, позволяющих пользователю легко рассчитать любой фильтр [1,2,11].

При рассмотрении вопросов реализации цифровых фильтров полезно изображать их в виде схем. Разностное уравнение (1.25) изображено на рис. 1.4. Подобные схемы, называемые структурными, описывают в графической форме те операции, которые необходимо проделать над входной последовательностью для получения сигнала на выходе.

Для фильтра после подстановки (1.49) в(1.51) и выполнения интегрирования получается

(1.52)

Импульсная характеристика (1.32) определена при любых целых значениях к и является бесконечной, поэтому ограничивают значения k . Пусть |k |≤К , где К =(N -1)/2 для фильтров с нечётными значениями N и К =N /2 для фильтров с чётными значениями N . Тогда конечная импульсная характеристика, соответствующая (1.52), записывается в виде