Дипломная работа: Разработка теории радиогеохимического эффекта

где m - интегральный параметр, удовлетворяющий закону аддитивности, - локальный параметр.

Выделим в пространстве неподвижную замкнутую поверхность ограничивающую объем . Каждой точке выделенного объема сопоставим вектор .

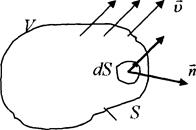
Рис.3.

Выберем на поверхности ориентированный элемент поверхности, где – вектор внешней нормали, - площадь выбранной площадки.

Тогда через элемент площади входит или выходит количество массы сплошной среды , где – вектор потока массы.

Через всю поверхность войдет или выйдет количество массы

(2.3)

Будем предполагать, что источники и стоки отсутствуют, тогда закон сохранения массы запишется в виде:

(2.4)

В (2.4) знак минус в правой части объясняется тем, что если образует с острый угол, т.е., то проходит через изнутри наружу, т.е. масса в убывает.

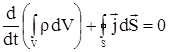(2.5)

Уравнение (2.5) – уравнение неразрывности для массы в интегральной форме.

Проведем в первом интеграле (2.5) дифференцирование по как по параметру (поскольку не зависит от ), т.е. внесем производную под знак интеграла и заменим ее частной производную, поскольку подынтегральная функция зависит от переменной интегрирования, получим:

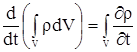(2.6)

Второй интеграл в равенстве (2.5) преобразуем в объемный, воспользовавшись теоремой Остроградского-Гаусса. Получим

(2.7)

где

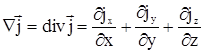Подставим (2.6), (2.7) в (2.5), и объединяя интегралы получим

(2.8)

Учитывая в (2.8) произвольность объема , получаем

(2.9)

Уравнение (2.9)– уравнение неразрывности для массы в дифференциальной форме.

2.2. Закон Фика

Закон Фика необходим для описания диффузии растворенного(радиоактивного) вещества пропорциональной градиенту их плотности. Плотность радиоактивных примесей является функцией от химического потенциала

В уравнении (2.9) предыдущего параграфа вектор потока имеет вид

(*)

где – конвекционная компонента вектора потока, связанная с потоком вещества (массы). Для случая, когда движение массы происходит только за счет конвекции, поток записывается в виде

(2.10)

– диффузионная компонента, возникает при наличии в системе градиента концентрации. Для диффузионного компонента справедлив I Закон Фика:

(2.10*)

– коэффициент концентрационной диффузии, (далее будем опускать).

Диффузионный поток пропорционален градиенту плотности, взятому с обратным знаком.

Подставим (2.10) и (2.10*) в (*), получим

(2.11)

Подставим (2.11) в (2.9), получим

(2.12)

В (2.12) каждое слагаемое записали отдельно:

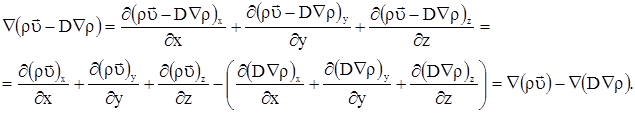Преобразуем второе слагаемое в (2.12):

(2.13)

Во втором слагаемом в (2.13) осуществим круговую перестановку (знак не меняется, т.к. скалярное произведение).

Из выражения (2.13), получим

(2.14)

Преобразуем второе слагаемое в (2.12):
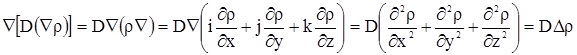