Физика / Дипломная работа: Разработка теории радиогеохимического эффекта

Дипломная работа: Разработка теории радиогеохимического эффекта

Подставив (2.14) и (2.15) в (2.12) получим

(2.16)

Если в (2.16) то получим уравнение диффузии (II Закон Фика):

(2.17)

2.3. Уравнение конвективной диффузии

Пусть имеется раствор с плотностью растворителя и плотностью растворенного вещества –, тогда плотность раствора запишется в виде

(2.18)

Запишем уравнение неразрывности для растворителя:

(2.19)

Диффузию не учитываем, потому что в жидкостях коэффициент диффузии мал.

Будем считать, что растворитель является несжимаемым, т.е. не зависит от пространственных координат и

(2.20)

Тогда из выражения (2.19), получим

(2.21)

Запишем уравнение неразрывности для раствора:

(2.22)

В (2.22) подставим (2.18), получим

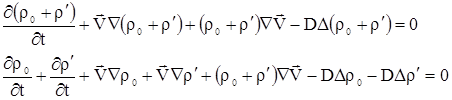Учитывая (2.20), (2.21) и независимость от пространственных координат, получим

(2.23)

Опустим штрих, предполагая в дальнейшем – плотность примеси.

(2.24)

Поясним в (2.24) значение каждого слагаемое:

Первое слагаемое описывает изменение массового содержания в рассматриваемой точке;

Второе слагаемое отвечает за конвекцию;

Третье слагаемое отвечает за диффузию.

Физический смысл уравнения (2.24) заключается в следующем: изменение концентрации, со временем, в рассматриваемой точке происходит за счет конвекции и диффузии.

На практике в (2.24) слагаемым можно пренебречь, в силу его малости.

2.4. Метод характеристик

Пусть движение несущей жидкости происходит вдоль оси , тогда уравнение без диффузионной конвекции запишется

(1)

Одномерное уравнение без диффузионной конвекции (или конвекционное уравнение).

Задача Коши для уравнения (1).

Требуется найти функцию , где и удовлетворяющую условиям:

(2)

Получим решение задачи методом характеристик.

Метод характеристик заключается в переходе от эйлеровых переменных и к лагранжевым. Связь производных в эйлеровых и лагранжевых координатах записывается в виде: