Дипломная работа: Разработка теории радиогеохимического эффекта
При 
,
 . | (11) |
Подставляя (11) в (3) получаем
 . |
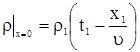Тогда решая систему
 |
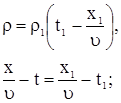получаем решение граничной задачи в виде
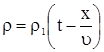 . | (12) |
В (12) 
.
Решение начально-краевой задачи будет иметь вид
 , |
где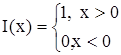 
, единичная функция Хевисайда.
Решение задачи Коши для неоднородного конвекционного уравнения
Построим формулу Даламбера для уравнения
 ,  ,  | (1) |
Уравнение (1) – уравнение эволюции локального параметра.
 . | (2) |
Тогда уравнение (1) запишем в виде системы двух уравнений:
 |
(3) (4) |
Интегрируя (4), получим
 | (5) |
Пусть при 
, 
, тогда
 . |
Подставим (5) в (3), получим
 . | |
 , | (6) |
 , | (7) |
| . | (8) |
Исключим в (6) 
для этого учтем начальное условие (7).
 , | |
 . | (9) |
Подставим (9) в (6), получим
 , | |
 . | (10) |
Исключим в (10) 
и 
, потом 
:
 . | (11) |
Выражение (11) – формула Даламбера (решение задачи Коши для неоднородного конвекционного уравнения).
Покажем что (11) является решением (1).
Продифференцируем формулу (11) по 
, получим
 . | (12) |
Продифференцируем формулу (11) по 
, получим
 . | (13) |
Подставляя (13) и (12) в (1), получаем
 . |
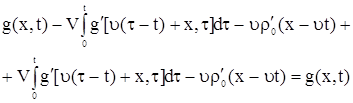Откуда получаем тождество: 
. Следовательно, выражение (11) является решением уравнения (1).
Начально-краевая задача для неоднородного конвективного уравнения
| , , | (1) |
| . | (2) |
 . | (3) |
Найдем решение граничной задачи для неоднородного конвекционного уравнения (1).
Решение будем искать в виде 
дифференцируя которое по ,получим
 . |
Умножая правую и левую части на 
, приходим к выражению
 . | (4) |
Перепишем уравнение (1) в виде двух уравнений:
 |
К-во Просмотров: 349
Бесплатно скачать Дипломная работа: Разработка теории радиогеохимического эффекта
|