Математика / Дипломная работа: Структура некоторых числовых множеств

Дипломная работа: Структура некоторых числовых множеств

Пусть

Обозначим через множество тех элементов А, для которых , где одно из возможных значений -го значка, т.е. положим

В силу сделанного допущения множество счетно, а так как

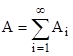, то счетно и А

Теорема доказана

Следствие 1. Множество точек плоскости, у которых обе координаты рациональны, счетно.

Следствие 2.Множество многочленов с целыми коэффициентами счетно.

Теорема 12. Множество алгебраических чисел счетно [6; 20].

§ 3. Мощность континуума

Теорема 1. Отрезок несчетен.

Доказательство

Допустим противное.

Пусть отрезок - счетное множество. Тогда все его точки можно расположить в виде последовательности

(1)

Пусть это сделано, т.е. всякая точка находится в последовательности (1).

Разделим на три равные части точками и (рис. 1). Ясно, что точка не может принадлежать всем трем отрезкам , , и хотя бы один из них не содержит ее. Обозначим через тот отрезок, который не содержит (если таких отрезков два, то через называем любой из них).

Рис. 1

Теперь разделим на три равных отрезка отрезок и обозначим через тот из новых отрезков, который не содержит точки .

Затем делим на три равных отрезка отрезок и обозначаем через тот из них, который не содержит точки и т.д.

В результате мы получим бесконечную последовательность вложенных друг в друга отрезков которые обладают тем свойством, что ,.

Так как длина отрезка с возрастанием стремиться к нулю, то по теореме Кантора о вложенных отрезках, существует точка , общая для всех отрезков , .

Так как , то точка должна входит в последовательность (1). Но это невозможно, ибо , . Отсюда получаем, что точка не может совпасть ни с одной из точек последовательности (1).