Дипломная работа: Структура некоторых числовых множеств

устанавливает взаимнооднозначное соответствие между множествами и , откуда и следует, что А имеет мощность континуума.

Так как удаление одного или двух элементов из бесконечного множества приводит к множеству, эквивалентному исходному, то промежутки , , имеет ту же мощность, что и отрезок , т.е. мощность с.

Теорема доказана.

Теорема 3. Сумма конечного числа попарно не пересекающихся множеств мощности с имеет мощность с.

Доказательство

Пусть

,

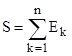где каждое из множеств имеет мощность с.

Возьмем полуинтервал и точками разложим его на полуинтервалов ,

Каждый из этих полуинтервалов имеет мощность с, так что мы можем связать множество и полуинтервал взаимнооднозначным соответствием. Легко видеть, что таким образом оказывается, установлено взаимнооднозначное соответствие между суммой и полуинтервалом

Теорема доказана.

Теорема 4. Сумма счетного множества попарно не пересекающихся множеств мощности с имеет мощность с.

Доказательство

Пусть

,

где каждое из множеств имеет мощность с.

Возьмем на полуинтервале монотонно возрастающую последовательность и точками для которой .

Установив взаимнооднозначное соответствие между множествами и для всех , мы тем самым установим взаимнооднозначное соответствие между и .

Теорема доказана.

Следствие 1. Множество всех действительных чисел имеет мощность с.

Следствие 2. Множество всех иррациональных чисел имеет мощность с.

Следствие 3. Существуют трансцендентные (неалгебраические) числа.

Теорема 5. Множество всех последовательности натуральных чисел

имеет мощность .

Доказательство

Докажем теорему двумя способами:

1) Основанное на теории непрерывных дробей.

Установим взаимнооднозначное соответствие между Р и множеством всех иррациональных чисел интервала (0, 1), считая взаимосоответствующими последовательность и иррациональное число , для которого разложение в непрерывную дробь имеет вид