Кристаллическая структура соединений системы Ni-Si

Соединение	Прототип	Параметры решетки, нм
		a	b	c
β (Ni3 Si)	AuCu3	0,350	─	─
β2 *1	(GePt3 ?)	0,697	0,625	0,507
β3 *2	(GePt3 ?)	0,704	0,626	0,508
δ (Ni2 Si)	Co2 Si	0,706	0,499	0,372
θ*3	─	0,3805	─	0,489
ε (Ni3 Si2 ) *4	─	1,2229	1,0805	0,6924
NiSi	MnP	0,562	0,518	0,334
αNiSi2	CaF2	0,546	─	─
*1 β=48,74о *2 β=48,84о *4 Ромбическая сингония

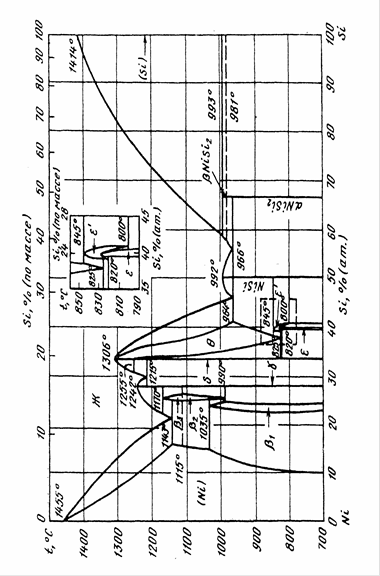
Рис.1.1 Диаграмма состояния системы Ni - Si.

1.3 Термодинамическое моделирование свойств твердых металлических растворов. Обобщенная теория "регулярных" растворов

Регулярный раствор образуется из компонентов с выделением или поглощением тепла, а энтропия смешения его такая же, как и в совершенном растворе. Проблема аналитического представления концентрационной и температурной зависимости термодинамических свойств сводится к поиску соответствующего выражения для избыточной энергии Гиббса G^E [5]. Обычно в качестве нулевого приближения к теории реальных растворов применяется модель идеального раствора, где G^E =0. В настоящей модели за нулевое приближение принята теория регулярных растворов.

Понятие "регулярный раствор" включает в себя как частные случаи понятия "идеальный" и "предельно разбавленный" раствор, а закон граничной регулярности, согласно которому любой раствор можно считать регулярным до определенного предела, справедлив для более широкого диапазона концентраций, чем законы Рауля и Генри [5].

Для регулярного раствора:

, (1.1)

где x_i и x_j - мольные доли компонентов,

Q_{ij -} энергия взаимообмена (смешения).

В рамках модели строго регулярного раствора энергии взаимообмена являются константами. В реальных системах энергии взаимообмена (как эмпирические параметры модели) зависят от состава и температуры.

Для субрегулярных растворов:

; (1.2)

Для квазирегулярных растворов:

; (1.3)

где: и - соответственно теплота и избыточная энтропия смешения компонентов. Выражения (1.2) и (1.3), очевидно, можно рассматривать как частные случаи неизвестной функции для концентрационной и температурной зависимостей энергии смешения компонентов, получаемой путем разложения и в ряд Тейлора. Если ограничиться несколькими первыми членами ряда:

; (1.4)

то получится представление функции полиномом. В свою очередь, каждый из параметров , , ,…, может зависеть от температуры:

; (1.5)

Многочлены (1.4) и (1.5) - приближенное выражение неизвестной функции . Качество приближения определяется величиной остатка рядов - той ее части, которая отбрасывается. Чтобы наше приближение удовлетворительно описывало термодинамические свойства раствора, нужно, чтобы остаток был невелик по сравнению с ошибкой экспериментов. Тогда дальнейшее уточнение функции теряет смысл.

Как показывает математическая обработка экспериментальных данных, для бинарных растворов достаточно трех параметров , , , чтобы в большинстве случаев корректно аппроксимировать термодинамические функции смешения системы. Поэтому концентрационную (конфигурационную) энергию взаимообмена компонентов в дальнейшем будем представлять тремя членами ряда (1.4), а избыточную энергию Гиббса любой фазы с областью гомогенности будем описывать уравнением:

; (1.6)

где и - термодинамические характеристики областей регулярности двойной системы вблизи чистых компонентов;

- параметр, учитывающий отклонение от "регулярности".

Умножив части уравнения (1.6) на общее число молей компонентов в растворе, получим избыточную энергию Гиббса произвольного количества фазы. Откуда:

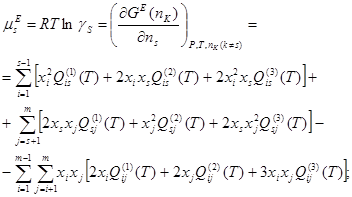(1.7)

Активности компонентов двойной системы: