Состав γ-фазы по диаграмме состояния Ni-Si

T, 0 С	T, К	xS i (γ)	xNi (γ)
793	1066	0,100	0,900
821	1094	0,105	0,895
870	1143	0,110	0,890
910	1183	0,115	0,885
933	1206	0,120	0,880
953	1226	0,125	0,875
974	1247	0,130	0,870
988	1261	0,135	0,865
1005	1278	0,140	0,860
1020	1293	0,145	0,855
1033	1306	0,150	0,850

Решая систему уравнений (1.19), получаем значения энергий смешения (табл.1.4). Q₁₂ <0, следовательно, раствор имеет отрицательные отклонения от закона идеальности.

Таблица 1.4

Энергии смешения для γ-фазы

№	T, К	Q12 , Дж/моль
1	1066	-165626,7
2	1094	-165257,0
3	1143	-163418,7
4	1183	-162127,0
5	1206	-161927,6
6	1226	-161878,5
7	1247	-161708,6
8	1261	-161963,2
9	1278	-161961,2
10	1293,	-162043,7
11	1306	-162211,6

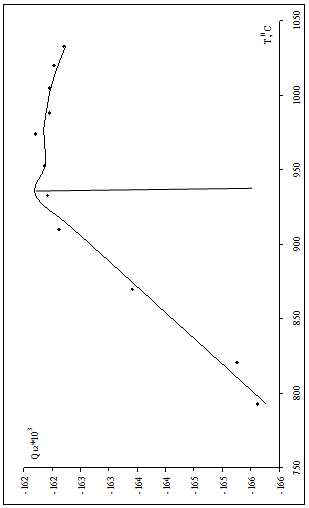
Рис.1.2 Зависимость энергии смешения от температуры.

Строим зависимость энергии смешения от температуры, аппроксимируем полученную функцию по частям (рис.1.2)

в области низких температур при мольной доле кремния 0,1-0,12 функцию зависимости энергии смешения аппроксимировали линейно:

, R² =0,9802; (1.20)

при мольной доле от 0,12 до 0,15 полиномиальная аппроксимация:

, R² =0,8098; (1.21)

1.5 Термодинамические функции образования интерметаллидов

Согласование энергий Гиббса образования бинарных интерметаллидов систем Ni - Si.

В системе Ni-Siпри низких температурах термодинамически устойчив твердый раствор кремния в никеле с решеткой г. ц. к., существуют интерметаллидные фазы β_{1 (} Ni₃ Si), δ (Ni₂ Si), ε (Ni₃ Si₂ ), αNiSi₂ и NiSi. Стандартные энергии Гиббса образования этих интерметаллидов приведены в таблице 1.5 [6].

Таблица 1.5.

Стандартные энергии Гиббса образования интерметаллидов

Соединение	, кДж/моль
β1 ( Ni3 Si)	-150,800
δ (Ni2 Si)	-143,100
ε (Ni3 Si2 )	-232,000
αNiSi2	-94, 200
NiSi	-89,600

1.6. Фазовые диаграммы состояния систем Ni-O и Si-O

Методы расчета фазовых диаграмм состояния металл-кислород.

Химическая устойчивость металлов в окислительной газовой среде, например, на воздухе, определяется их стойкостью к окислению кислородом. Лучшим способом представления термодинамической информации об окислении металлических материалов являются фазовые диаграммы состояния систем металл-кислород.

На фазовых диаграммах Ме-О представлены различные химические равновесия, играющие роль в процессе окисления металла. Они характеризуют растворимость кислорода в данном металле, состав оксидных форм, образующихся в результате окислении металла кислородом, и устойчивость фаз в зависимости от различных параметров системы: температуры, давления, состава и др.

Состав системы выражается содержанием металла и кислорода в атомных процентах, либо в процентах по массе.

Для более сложных систем, содержащих третий компонент - другой металл, существуют аналогичные диаграммы состояния Ме₁ -Ме₂ -О. Они позволяют разобраться в вопросах состава и структуры окалины (слоев окислов) на поверхности бинарных сплавов. В литературе накоплен огромный справочный материал по термодинамическим свойствам неорганических веществ, сформулированы общие принципы фазовых равновесий в гетерогенных системах (правило фаз Гиббса), предложены различные модели, интерполирующие свойства компонентов и металлических, и оксидных растворов (теории совершенных и "регулярных" растворов) и т.п. Все это позволило расчетным путем выявить вид и характерные особенности интересующих нас диаграмм состояния [7].

Согласно закону равновесия фаз - правилу фаз Гиббса, в трехкомпонентной системе при постоянных внешних параметрах (P,T=const):

f=3-Ф; (1.22)

где f - число термодинамических степеней свободы, или вариантность системы, то есть количество параметров (температура, давление, концентрации компонентов в фазах), которые являются независимыми,

Ф - количество фаз в системе, находящихся в равновесии.

Из физических соображений следует, что f0. Таким образом, в указанной системе возможны равновесия с участием одной, двух или максимум трех фаз:

однофазные равновесия (f=2); отдельные фазы (вещества) термодинамически устойчивы в определенном интервале составов и, соответственно, парциальных давлений кислорода;

двухфазные (моновариантные) равновесия (f=1);

трехфазные (нонвариантные) равновесия (f=0).

В условиях трехфазного равновесия система не имеет степеней свободы, т.е. данное состояние системы полностью описывается законами действующих масс гетерогенных химических реакций и условиями нормировки составов фаз. Для однозначного расчета составов фаз в условиях двухфазового равновесия необходимо задаваться одним из параметров системы.