Дипломная работа: Устойчивость по Ляпунову

Рассмотрим систему дифференциальных уравнений

Выделим некоторое решение системы и назовем его невозмущенным решением.

Решение назовем устойчивым в смысле Ляпунова, если для любого можно указать такое, что из неравенства следует неравенство при . Здесь через обозначено любое другое решение системы , определяемое начальным условием . Решение называется асимптотически устойчивым в смысле Ляпунова, если оно устойчиво в смысле Ляпунова и если существует такое , что при будем иметь

Пример Решение уравнения не является устойчивым ни справа, ни слева, т.к. каждое решение , где (), перестает существовать при (рис. 1).

Пример. Решение уравнения неустойчиво справа, т.к. все решения , , , приближаются к при . Каждое решение так же, как и решение , является асимптотически устойчивым справа (рис. 2).

Проведем в системе замену переменных . Новая система будет иметь вид

вводя обозначение

получим систему

где при . Решение перешло при рассматриваемой замене переменных в положение равновесия новой системы. Задача устойчивости решения переходит, таким образом, в задачу устойчивости нулевого (тривиального) решения системы .

Приведем определение устойчивости нулевого решения системы .

Решение системы называется устойчивым в смысле Ляпунова, если для любого можно указать такое, что из неравенства следует неравенство при . Если же, кроме того, всякое решение , начальные данные которого определяются условием , обладает свойством , то нулевое решение называется асимптотически устойчивым в смысле Ляпунова.

Метод функций Ляпунова. Теоремы Ляпунова

Проиллюстрируем идею метода на простейшем примере:

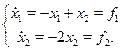
Рассмотрим функцию . Эта функция положительна всюду, кроме точки , где она обращается в нуль. В пространстве переменных уравнение определяет параболоид с вершиной в начале координат. Линии уровня этой поверхности на плоскости представляют собой эллипсы. Зададим произвольно малое . Построим на плоскости круг радиуса . Возьмем одну из линий уровня --- эллипс, целиком лежащий внутри круга . Построим другой круг целиком лежащий внутри эллипса (рис. 3).

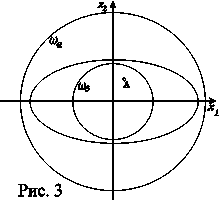
Пусть начальная точка лежит внутри .

Рассмотрим функцию двух переменных . Легко видеть, что если вместо подставить решение системы , то полученная таким образом, функция от будет представлять собой полную производную функции вдоль траектории решения системы . Если эта производная вдоль любой траектории, начинающейся в , неположительна, то это будет означать, что траектория не сможет покинуть , так как иначе между и значением , при котором она попадет на границу , найдется значение , для которого , поскольку . То, что ни одна траектория, начинающаяся в , не покидает ни при одном круг , означает устойчивость тривиального решения.

Итак, мы должны проверить знак вдоль траектории. Для этого надо знать саму траекторию. Хотя в данном примере это можно сделать, но метод должен быть рассчитан на систему общего вида, для которого нельзя выписать явно и тем самым нельзя проверить нужное неравенство. Поэтому мы будем требовать, чтобы функция была неположительной как функция двух независимых переменных по крайней мере в некоторой окрестности . Это условие можно проверить непосредственно по правым частям системы не зная решения. В нашем примере именно так и будет, поскольку всюду на плоскости , а тем самым вдоль любой траектории, и устойчивость тривиального решения гарантирована. Функция и есть функция Ляпунова для рассмотренного примера. Она имеет вид квадратичной формы, хотя в принципе можно было взять любую другую функцию, лишь бы она была положительной всюду, кроме точки , где она обращается в нуль, а выражение было неположительное. Обратимся теперь к формулировке некоторых общих теорем, в основу которых положена эта идея. Будем исследовать тривиальное решение системы .

Все дальнейшие построения будем вести в некоторой -окрестности начала координат в фазовом пространстве. Пусть для определенности задается неравенством , . Функция (или короче ) называется положительно определенной в , если в , причем тогда и только тогда, когда .

Приведем ряд утверждений, показывающих применение функций Ляпунова .

Теорема Первая теорема Ляпунова

Пусть в существует непрерывная вместе с частными производными первого порядка положительно определенная функция такая, что функция удовлетворяет неравенству