Доклад: Графика в системе Maple V

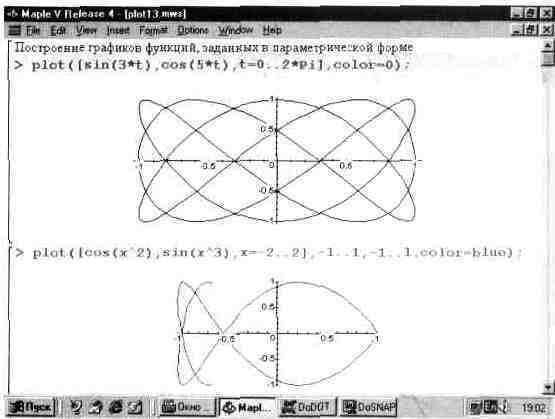
Рис. 13.13. Построение функции, заданных параметрически.

13.2.12. Построение графиков функций в полярной системе координат

Графики в полярной системе координат представляют собой линии, которые описывает конец радиус вектора r(t) при изменении угла t в определенных пределах — от tmin до tmax. Построение таких графиков производится также функцией plot, которая записывается в следующем виде:

plot([r(t),theta(t),t=tmin..tmax],h,v,p,coords=polar)

Здесь существенным моментом является задание полярной системы координат опцией coords=polar. Рис. 13.14 дает примеры построения графиков функций в полярной системе координат.

Графики параметрических функций и функций в полярной системе координат отличаются огромным разнообразием. Снежинки и узоры мороза на стеклах, некоторые виды кристаллов и многие иные физические объекты подчиняются математическим закономерностям, положенным в основу построения таких графиков.

13.3. Построение ЗО-графиков с помощью функция plot3d

13.3.1. Особенности применения функции plot3d

Для построения графиков трехмерных поверхностей Maple имеет встроенную в ядро функцию plot3d. Она может использоваться в следующих форматах:

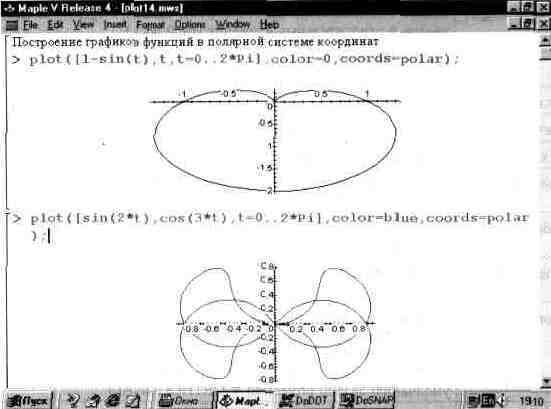
Рис. 13.14. Построение графиков функций в полярной системе координат.

plot3d(exprl, x=a..b, y=c..d,p) plot3d(f, a..b, c..d,p)

plot3d([exprf,exprg,exprh], s=a..b, t=c..d,p) plot3d([f,g,h], a..b, c..d,p).

В двух первых формах plot3d применяется для построения обычного графика одной поверхности, в других формах — для построения графика с параметрической формой задания поверхности. В приведенных формах: f, g и h — функции, expri — выражение, отражающее зависимость от х и у, exprf, exprg и exprh — выражения, задающие поверхность параметрически, s, t, а и b — числовые константы действительного типа, end — числовые константы или выражения действительного типа, х, у, s и t — имена независимых переменных и р — параметры-опции. Параметры для функции plot3d задаются аналогично их заданию для функции plot.

13.3.2. Параметры функции plot3d

С помощью параметров р можно в широких пределах управлять видом трехмерных графиков, выводя или убирая линии каркасной сетки, вводя функциональную окраску поверхностей, меняя угол их обзора и параметры освещения, изменяя вид координатных осей и т.д.

Следующие параметры функции plot3d задаются аналогично их заданию для функции plot:

axesfont font color coords font labelfont linestyle numpoints scaling style symbol thickness title titlefont

Однако функция plot3d имеет ряд дополнительных специфических параметров:

ambientlight=[r,g,o]	Задает интенсивность красного (red), зеленого (green) и синего (blue) цветов в относительных единицах (от 0 до 1).
axes=f	Задает вид координатных осей (BOXED, NORMAL, FRAME и NONE, по умолчанию NONE).
grid=[m,nl	Задает число линии каркаса поверхности.
gridstyle=x	Задает стиль линий каркаса х ( 'rectangular' или 'triangular').
labels=[x,y,z]	Задает надписи по осям (х, у и z — строки, по умолчанию пустые).
light=[phi,theta,r,g, b]	Задает углы, под которыми расположен источник освещения поверхности и интенсивности составляющих (г, g и b) цвета.
lightmodel=x	Задает режим яркости (соответственно, none", 'lightl', 'light2', 'light3' и 'light4').
orientation=[theta, phi]	Задает углы ориентации поверхности (по умолчанию 45 градусов).
projection=r	Задает перспективу при обзоре поверхности (г может быть числом 0 или 1, задающим включение или выключение перспективы, а также одной из строк 'FISHEYE', 'NORMAL', или 'ORTHOGONAL' (это соответствует численному значению г 0, 0.5, или 1, соответственно, причем по умолчанию задано projection = ORTHOGONAL).
shading=s	Задает направления, по которым меняется цвет функциональной окраски (значения s могут быть XYZ, XY, Z, ZGREYSCALE, ZHUE, NONE).
tickmarks=[l,n,m]	Задает характер маркировки по осям х, у и z (числа 1, п и m имеют значения не менее 1).
view=zmin..zmax или Ixmin..xmax,ymin.. ymax,zmin..zmax]	Задает минимальные и максимальные координаты поверхности для ее видимых участков.

13.3.3. Выбор и пересчет координат ЗО-графиков

Для трехмерных графиков возможно задание 31-го типа координатных систем с помощью параметра соога5=Тип_координатнои_системь1. Поскольку на экране дисплея поверхность отображается только в прямоугольной системе координат и характеризуется координатами х, у и z, то для представления поверхности, заданной в иной системе координат с координатами u, v и w используются известные [46,47] формулы для преобразования (u, v, w) --> (х, у, z). Ниже представлены типы координатных систем для трехмерной графики и соответствующие формулы преобразования:

bipolarcylindrical

х = a*sinh(v)/(cosh(v)-cos(u)) у = a*sin(u)/(cosh(v)-cos(u)) z = w

bispherical

х = sin(u)*cos(w)/d у = sin(u)*sin(w)/d z = sinh(v)/d (где d = cosh(v) - cos(u) )

cardiodal

x = u*v*cos(w)/(lГ2+v»2)-2 у = u*v*sin(w)/(ir2+v"2r2 z = (u"2-v'2)/2/^2+v'2)-2

cardiodcylindrical

x = (u'2-v~2)/2/(u'-2+v~2)'-2 у = u*v/(u'2+v-2)"2 z = w

casscylindrical