Доклад: Графика в системе Maple V

paraboloidal

x = u*v*cos(w) у = u*v*sin(w) z = (u"2 - v'2)/2

paraboloidal2

x = 2*((u-a)*(a-v)*(a-w)/(a-b))-(l/2) у = 2*((u-b)*(b-v)*(b-w)/(a-b))-(l/2) z = u+v+w—a—b

paracylindrical

x = (u'2 - v'2)/2 у = u*v z = w

prolatespheroidal

x = a*sinh(u)*sin(v)*cos(w) y=a*sinh(u)*sin(v)*sin(w) z=a*cosh(u)*cos(v)

rectangular

x = и у = v • z = w

rosecylindrical

x = ((1Г2+у-2)-(1/2)+и)-(1/2)/(1Г2+у-2Г(1/2) у = ((u'2+v'2y(l/2)-uY(l/2)/(u'2+v'2V(\/2) z = w

sixsphere

x= u/(u'2+v'2+w'2) у = v/(u'-2+v'2+v/''2) z = w/(u'2+v'2+w'2)

spherical

x = u*cos(v)*sin(w) у = u*sin(v)*sin(w) z = u*cos(w)

tangentcylindrical

x = u/(ir2+v"2) у = v/(u«2+v»2) z = w

tangentsphere

x = u-costwVdj^+v^) у = u*sin(w)/(ir2+v"2) z = v/(u"2+v~2)

toroidal

x = a*sinh(v)*cos(w)/d у = a*sinh(v)*sin(w)/d z = a*sin(u)/d (где d = cosh(v) - cos(u) )

Эти формулы полезно знать, поскольку в литературе встречаются несколько отличные формулы пересчета.

Вид графиков трехмерных поверхностей очень сильно различается в разных

координатных системах. По умолчанию трехмерные графики строятся в прямоугольной системе координат — rectangular.

13.4. Примеры построения трехмерных поверхностей с помощью функции plot3d

13.4.1. Простейшее построение ЗО-поверхности с разным стилем

На рис. 13.15 показано два примера простейших построений графиков трехмерной поверхности. По умолчанию строится каркасная поверхность с функциональной окраской тонких линий каркаса и удалением невидимых линий. Чтобы график выглядел более четким, построение в первом примере задано линиями черного цвета с помощью параметра color-black.

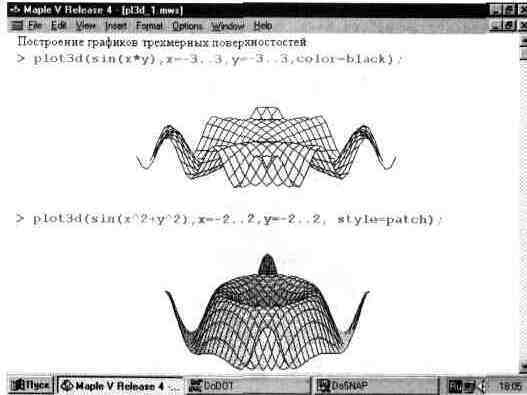
Рис. 13.15. Примеры простейшего построения трехмерных поверхностей.