Книга: Элективный курс по математике для классов спортивно-оборонного профиля

3.Разность
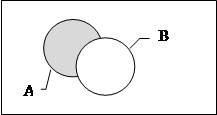
Разностью событий A-B называется событие C, состоящее из всех э событий, входящих в A, но не входящих в B.
4.Противоположное
Событие называется противоположным событию A, называется событие, состоящее в непоявлении события А. Обозначается противоположное событие символом ![]() .
.
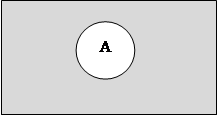
Пример: Противоположными событиями являются промах и попадание при выстреле, или выпадении герба или цифры при одном подбрасывании монеты.
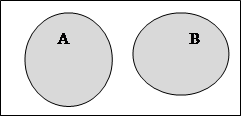
5.События A и B называются несовместными , если они никогда не могут произойти в результате одного испытания.
Пример: При одном подбрасывании монеты никогда не выпадет одновременно и орел и цифра.
6.События называется невозможным, если оно не может произойти в результате данного испытания. Принято обозначение: ![]() Ø.
Ø.
7.Достоверное событие
Событие называется достоверным, если оно обязательно произойдет в результате данного испытания. Оно обозначается как Е.
![]()

1.2 Вероятность событий
Рассмотрим некоторое количество испытаний, в результате которых появилось событие А. Пусть было произведено N испытаний, в результате которых событие А появилось ровно n раз. Тогда отношение ![]() - называют относительной частотой (частость).
- называют относительной частотой (частость).
Также при большом количестве повторений испытания частость событий мало изменяется и стабилизируется около определенного значения, а при не большом количестве повторений она может принимать различные значения. Поэтому интуитивно ясно, что при большом количестве повторений испытания частость события будет стремиться к определенному числовому значению. Такое значение принято называть вероятностью события А и обозначают Р(А).
В математике неограниченное число поворений принято записывать в виде предела при N стремящегося к бесконечности:
![]()
Так как n всегда больше либо равно N, то вероятность заключена в интервале: ![]() .
.
В некоторых случая вероятности событий могут быть легко определены исходя из условий испытаний. Пусть испытание имеет n возможных исходов, то есть событий, которые могут появиться в результате данного испытания. При каждом повторении возможно появление только одного из данных исходов (то есть все n исходов несовместны). Кроме того по условиям испытания нельзя сказать какие исходы появляются чаще других, то есть все исходы являются равновозможными. Допустим теперь что при n равновозможных исходах интерес представляет событие А, которое появляется только при m исходах и не появляется при остальных n-m исходах. И принято говорить, что в данном испытании имеется n случае, из которых m благоприятствуют появлению события А.
В таком случае вероятность можно вычислить, как отношение числа случаев благоприятствующих появлению события А (т.е. m), к общему числу всех исходов n:
![]() .
.
Данная формула представляет собой определение вероятности по Лапласу, которое пришло из области азартных игр, где теория вероятности применялась для определения перспективы выигрыша.
1.3 Основные формулы комбинаторики
Для того чтобы определить вероятность нужно знать количество исходов, а также количество благоприятных исходов. Если количество испытаний мало, то можно вручную перебрать все исходы и выявить среди них благоприятные. Что делать в том случае, если количество испытаний велико?
В таком случае приходят на помощь следующие формулы.
Теорема о перемножении шансов :
Пусть имеется, k групп элементов, причем каждая группа элементов содержит определенное количество элементов, например 1-ая содержит n 1 элемент, 2-ая группа n 2 элементов, тогда i -я группа содержит ni элементов. Тогда общее число N способов, которыми можно произвести такой выбор, равняется
![]()