X

a₁

a₂

a₃

x₁

a₂

a₃

a₁

x₂

a₁

a₁

a₂

Таблица 1.9.

a1	an
a1	xj (yk )
an	x| (ym )

При графическом способе задания абстрактные автоматы представляются ориентированными графами. Графом автомата называется ориентированный связный граф, вершины которого соответствуют состояниям автомата, а дуги между ними - переходам между состояниями. Две вершины a_k и a_s соединяются дугой в том случае, если в автомате имеется переход из состояния a_k в состояние a_s . Для автомата Мили входной и выходной сигналы проставляются на дуге, соответствующей данному переходу (рис 1.3.), для автомата Мура входной сигнал проставляется на дуге, а выходной - рядом с вершиной, соответствующей состоянию (рис 1.4.).

Здесь рассматриваются только детерминированные автоматы, у которых выполнено условие однозначности переходов: автомат, находящийся в некотором состоянии, под действием любого входного сигнала не может перейти более чем в одно состояние. Применительно к графическому способу задания автомата это означает, что в графе автомата из любой вершины не могут выходить две и более дуги, отмеченные одним и тем же входным сигналом.

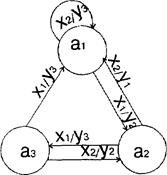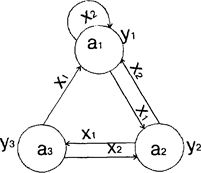Рисунок 1.3-Граф автомата Мили Рисунок 1.4-Граф автомата Мура

При аналитическом способе задания абстрактные автоматы задаются четверкой объектов:

S={ X,A,Y,F}, где Fзадает для каждого состояния а_j автомата отображение (ХхА) - > (AxY). Другими словами, при аналитическом способе задания для каждого состояния автомата а_j указывается отображение F_ai , представляющее собой множество всех троек а_р , x_m , y_k , и таких, что под воздействием входного сигнала x_m автомат переходит из состояния а _j в состояние а_р , выдавая при этом выходной сигнал y_k .

Применительно к общему определению абстрактного автомата, последнее равнозначно описанию функций δи λв соответствии с выражением: a_p = δ (a_i , x_m ), y_к = λ (a_i , x_m ).

Отображение F_ai записывается следующим образом:

F_ai {a_p (X_m /y_k ),a_i (X_f /y_z ) …}.

Для абстрактного автомата Мили (табл.1.7.) аналитическое задание имеет следующий вид:

S={ X,A,Y,F}, X={x₁ ,x₂ }, A={a₁ , а₂ , а₃ }, Y={y₁ , y₂ , у₃ },

F_a1 ={a₂ (x₁ /y₂ ), a₁ (x₂ /у₃ ) },

F_{а 2} ={а₃ (x₁ /y₃ ), a₁ (x₂ /y₁ ) },

F_{a 3} ={a₁ (x₁ /y₃ ), а₂ (x₂ /y₂ ) }.

Следует отметить, что функция F_ai всегда записывается для исходного состояния.

Определим синхронные и асинхронные автоматы. Состояние а_s автомата Sназывается устойчивым cостоянием, если для любого входного сигнала х_j Х, такого, что а_s = δ (а_i Х_m ) имеет место a_s = δ (a_s , x_m ).

Автомат S называется асинхронным, если каждое его состояние a_s А устойчиво. Автомат S называется синхронным, если он не является асинхронным.

Необходимо заметить, что построенные на практике автоматы всегда асинхронные и устойчивость их состояний всегда обеспечивается тем или иным способом, например, введением сигналов синхронизации. Однако, на уровне абстрактной теории автоматов, когда автомат всего лишь математическая модель, которая не отражает многих конкретных особенностей его реализации, часто оказывается более удобным оперировать с синхронными автоматами.

1.4 Связь между моделями Мили и Мура