Пусть абстрактный автомат Мили задан графом рис.1.5.

На вход этого автомата, установленного в начальное состояние, поступает входное слово X=x₁ , x₁ , x₂ , x₁ , x₂ , x₂ .

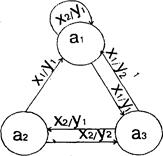
Рисунок 1.5 - Граф автомата Мили

Так как  (a₁ , x₁ ) = а₃ , a (a₁ , x₁ ) = y₁ , то под действием первой буквы слова Х входного сигнала x₁ автомат перейдет в состояние a₃ и на выходе его появится сигнал y_1. Далее,  (а₃ , x₁ ) = a₁ , а  (а₃ , x₁ ) = у₂ , потому при приходе второго сигнала x₁ автомат окажется в состоянии a₁ , а на выходе его появится сигнал у₂ . Проследив непосредственно по графу или таблицам переходов и выходов дальнейшее поведение автомата, опишем его тремя строчками, первая из которых соответствует входному слову X, вторая - последовательности состояний, которые проходит автомат под действием букв слова X, третья - выходному слову У, которое появляется на выходе автомата:

x₁ x₁ x₂ x₁ x₂ x₂

a₁ а₃ a₁ a₁ а₃ a₂ а₃

y₁ y₂ y₁ y₁ y₁ y₂

Назовем у =  (а₁ , X) реакцией автомата Мили в состоянии a₁ на входное слово X. Как видно из примера, в ответ на входное слово длины kавтомат Мили выдает последовательность состояний длины к+1 и выходное слово длины k. В общем виде поведение автомата Мили, установленного в состояние а_m , можно описать следующим образом:

Входное слово	xi 1	xi 2	xi 3
Последовательность состояний	am	ai2 = (am ,xi1 )	ai3 = (ai2 ,xi2 ).
Выходное слово	yi 1 = (am ,xi 1 )	yi2 = (ai2 ,xi2 )	yi3 = (ai3 ,xi3 )

Точно так же можно описать поведение автомата Мура, находящегося в состоянии a_m , при приходе входного слова x_{i 1} , x_i2 ,., х_ik . Напомним, что в соответствии с (1-2) выходной сигнал в автомате Мура в момент времени t (У (t)) зависит лишь от состояния, в котором находится автомат в момент t (a (t)):

Входное слово	xi 1	xi 2	xi 3
Последовательность состояний	am	ai2 = (am ,xi1 )	ai3 = (ai2 ,xi2 )	ai4 = (ai3 ,xi3 )
Выходное слово	yi 1 = (am ,xi 1 )	yi2 = (ai2 ,xi2 )	yi3 = (ai3 ,xi3 )	yi 4 = (ai 4 )

Очевидно, что выходной сигнал у_i1 =λ (a_m ) в момент времени i₁ не зависит от входного сигнала x_{i 1} , а определяется только состоянием а_m .

Таким образом, этот сигнал y_{i 1} никак не связан с входным словом, поступающим на вход автомата, начиная с момента i₁ . В связи с этим под реакцией автомата Мура, установленного в состояние a_m на входное слово X=x_{i 1} , х_i2 ,., х_ik будем понимать выходное слово той же длины у= λ (a_m ,Х) =у_i2 , у_i3 ,., y_{ik +1} .

В качестве примера рассмотрим автомат Мура S5, граф которого изображен на рис.1-6, и найдем его реакцию в начальном состоянии на то же самое входное слово которое мы использовали при анализе поведения автомата Мили S1:

Входное слово	x1	x1	x2	x1	x2	х2
Последовательность состояний	a1	a4	a1	a1	a4	a3	a5
Выходное слово	y1	y1	y2	y1	y1	y1	y2

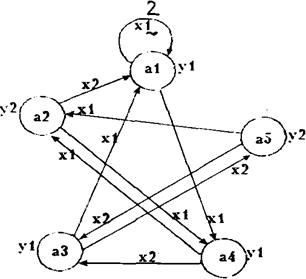
Рисунок 1-6 - Граф автомата Мура

Как видно из этого и предыдущего примеров, реакции автоматов S5 и S1 в начальном состоянии на входное слово Х с точностью до сдвига на 1 такт совпадают (реакция автомата Мура обведена линией). Дадим теперь строгое определение эквивалентности полностью определенных автоматов.

Два автомата S_A и S_B с одинаковыми входными и выходными алфавитами называются эквивалентными, если после установления их в начальные состояния их реакции на любое входное слово совпадают.

1.5 Эквивалентные автоматы. Эквивалентные преобразования автоматов

Можно показать, что для любого автомата Мили существует эквивалентный ему автомат Мура и, обратно, для любого автомата Мура существует эквивалентный ему автомат Мили.

При описании алгоритмов взаимной трансформации автоматов Мили и Мура в соответствии с изложенным выше мы будем пренебрегать в автоматах Мура выходным сигналом, связанным с начальным состоянием ( (a₁ )).

Рассмотрим сначала преобразование автомата Мура в автомат Мили.

Пусть дан автомат Мура: S_A ={ Х_A , А_A , У_A ,_A ,_A , а_{о A} }, где:

Х_A ={х₁ , х₂ ,. х_n }; Y={y₁ , у₂ ,. у_m }; А={ а₀ , а₁ , а₂ ,. а_N }; а_{0 A} = а_{0 -} начальное состояние (а_{0 A} А); _A - функция переходов автомата, задающая отображение (Х_A хА_A ) - >А_A ; _A - функция выходов автомата, задающая отображение А_A ->У_A .

Построим автомат Мили: S_B ={ Х_B , А_B , Y_B ,_B , _B , а_{0 B} }, у которого А_B =А_A ; Х_B =Х_A ; Y_B =У_A ; _B =_A ; а_{0 B} =а_{0 A.} Функцию выходов _B определим следующим образом. Если в автомате Мура _A (а_m , х₁ ) = а_s и _A (а_s ) =y_g , то в автомате Мили _B (a_{m ,} х₁ ) =y_g

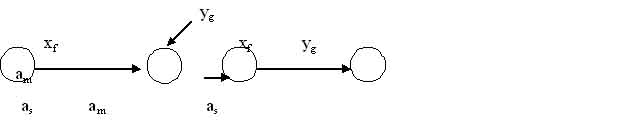
Рисунок 1.7 - Иллюстрация перехода от модели Мура к модели Мили

Переход от автомата Мура к автомату Мили при графическом способе задания иллюстрируется рис.1-7: выходной сигнал y_g записанный рядом с вершиной (a_s ), переносится на все дуги, входящие в эту вершину.

При табличном способе задания автомата таблица переходов автомата Мили совпадает с таблицей переходов исходного автомата Мура, а таблица выходов получается из таблицы переходов заменой символа a_s , стоящего на пересечении строки х_f и столбца а_m , символом выходного сигнала y_g отмечающего столбец a_s в таблице переходов автомата S_A .

Из самого способа построения автомата Мили S_B очевидно, что он эквивалентен автомату Мура S_A . По индукции нетрудно показать, что любое входное слово конечной длины, поданное на входы автоматов S_A и S_B , установленных в состояния a_m , вызовет появление одинаковых выходных слов и, следовательно, автоматы S_A и S_B эквивалентны.

Прежде чем рассмотреть трансформацию автомата Мили в автоматМура, наложим на автомат Мили следующее ограничение: у автомата не должно быть преходящих состояний. Под преходящим будем понимать состояние, в которое при представлении автомата в виде графа не входит ни одна дуга, но которое имеет по крайней мере одну выходящую дугу. Итак, пусть задан автомат Мили: