Контрольная работа: Экономическое моделирование
Поскольку доля остаточной дисперсии в общей составила 18%, поэтому уравнение регрессии объясняется 82% дисперсии результативного признака, т. е. коэффициент детерминации равен R2 = 0,82.
Индекс корреляции находится: 
Величина индекса корреляции достаточно близка к 1 и означает наличие достаточно тесной связи объема спроса от размера цены.
F –тест состоит в проверке гипотезы H0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого сравнивается фактическое и критическое значение F-критерия Фишера. При уровне значимости α = 0,05, k1 = 1 (m) и k2 = 20 (n-m-1=20-1-1) степенях свободы табличное значение F-критерия Фишера 
:
.
> 
,
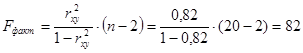то H0 – гипотеза о случайной природе оцениваемых характеристик откланяется и признается их статистическая значимость и надёжность.
Вывод: уравнение регрессии характеризует достаточно тесную зависимость спроса на товар K от его цены. Причем, наблюдается обратная зависимость: с увеличением цены, спрос падает.
Задача 4
Изучение влияния стоимости основных и оборотных средств на величину валового дохода торговых предприятий. Для этого по 12 торговым предприятиям были получены данные, приведенные в таблице:
| Номер предприятия | Валовой доход за год, млн.руб. | Среднегодовая стоимость, млн.руб. | |
| основных фондов | оборотных средств | ||
| 1 | 203 | 118 | 105 |
| 2 | 63 | 28 | 56 |
| 3 | 45 | 17 | 54 |
| 4 | 113 | 50 | 63 |
| 5 | 121 | 56 | 28 |
| 6 | 88 | 102 | 50 |
| 7 | 110 | 116 | 54 |
| 8 | 56 | 124 | 42 |
| 9 | 80 | 114 | 36 |
| 10 | 237 | 154 | 106 |
| 11 | 160 | 115 | 88 |
| 12 | 75 | 98 | 46 |
Задание
1. Постройте линейное уравнение множественной регрессии и поясните экономический смысл его параметров. Оцените статистическую значимость параметров регрессионной модели с помощью t-критерия.
2. Рассчитайте средние коэффициенты эластичности.
3. Определите парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделайте выводы о силе связи результата и факторов.
4. Дайте оценку полученного уравнения на основе общего F-критерия Фишера.
5. Оцените качество уравнения через среднюю ошибку аппроксимации.
6. Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
7. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение.
Построение линейной множественной регрессии сводится к оценке ее параметров – а, b1 и b2. Для расчета параметров а, b1 и b2 уравнения регрессии 
решаем систему нормальных уравнений относительно а, b1 и b2 :
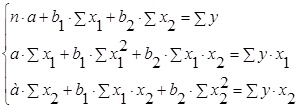
По исходным данным произведем расчет предварительных параметров (табл. 4.1)
Таблица 4.1
| № | У | Х1 | Х2 | Х1 2 | Х2 2 | Х1 ·Х2 | У·Х1 | У·Х2 | ŷ |
| 1 | 203 | 118 | 105 | 13924,00 | 11025,00 | 12390,00 | 23954,00 | 21315,00 | 197,29 |
| 2 | 63 | 28 | 56 | 784,00 | 3136,00 | 1568,00 | 1764,00 | 3528,00 | 80,63 |
| 3 | 45 | 17 | 54 | 289,00 | 2916,00 | 918,00 | 765,00 | 2430,00 | 73,07 |
| 4 | 113 | 50 | 63 | 2500,00 | 3969,00 | 3150,00 | 5650,00 | 7119,00 | 100,80 |
| 5 | 121 | 56 | 28 | 3136,00 | 784,00 | 1568,00 | 6776,00 | 3388,00 | 44,39 |
| 6 | 88 | 102 | 50 | 10404,00 | 2500,00 | 5100,00 | 8976,00 | 4400,00 | 98,90 |
| 7 | 110 | 116 | 54 | 13456,00 | 2916,00 | 6264,00 | 12760,00 | 5940,00 | 110,97 |
| 8 | 56 | 124 | 42 | 15376,00 | 1764,00 | 5208,00 | 6944,00 | 2352,00 | 93,91 |
| 9 | 80 | 114 | 36 | 12996,00 | 1296,00 | 4104,00 | 9120,00 | 2880,00 | 80,01 |
| 10 | 237 | 154 | 106 | 23716,00 | 11236,00 | 16324,00 | 36498,00 | 25122,00 | 212,75 |
| 11 | 160 | 115 | 88 | 13225,00 | 7744,00 | 10120,00 | 18400,00 | 14080,00 | 167,62 |
| 12 | 75 | 98 | 46 | 9604,00 | 2116,00 | 4508,00 | 7350,00 | 3450,00 | 90,66 |
| Итого: | 1351,00 | 1092,0 | 728,0 | 119410,0 | 51402,0 | 71222,0 | 138957,0 | 96004,0 | 1351,00 |
Систему линейных уравнений удобно решать методом Крамера (метод определителей):
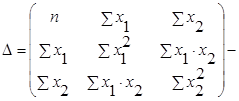
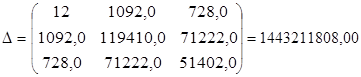
- частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
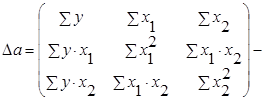
частный определитель параметра а.