Контрольная работа: Экономическое моделирование
Парный коэффициент корреляции между у и х2 рассчитывается по формуле:
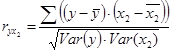
Произведем расчет необходимых параметров в таблице 4.3
Таблица 4.3
| № | У | Х2 |  |  |  |  |  |
| 1 | 203,0 | 105,0 | 90,4 | 44,3 | 4008,47 | 8175,17 | 1965,44 |
| 2 | 63,0 | 56,0 | -49,6 | -4,7 | 231,39 | 2458,51 | 21,78 |
| 3 | 45,0 | 54,0 | -67,6 | -6,7 | 450,56 | 4567,51 | 44,44 |
| 4 | 113,0 | 63,0 | 0,4 | 2,3 | 0,97 | 0,17 | 5,44 |
| 5 | 121,0 | 28,0 | 8,4 | -32,7 | -274,94 | 70,84 | 1067,11 |
| 6 | 88,0 | 50,0 | -24,6 | -10,7 | 262,22 | 604,34 | 113,78 |
| 7 | 110,0 | 54,0 | -2,6 | -6,7 | 17,22 | 6,67 | 44,44 |
| 8 | 56,0 | 42,0 | -56,6 | -18,7 | 1056,22 | 3201,67 | 348,44 |
| 9 | 80,0 | 36,0 | -32,6 | -24,7 | 803,72 | 1061,67 | 608,44 |
| 10 | 237,0 | 106,0 | 124,4 | 45,3 | 5640,22 | 15479,51 | 2055,11 |
| 11 | 160,0 | 88,0 | 47,4 | 27,3 | 1296,06 | 2248,34 | 747,11 |
| 12 | 75,0 | 46,0 | -37,6 | -14,7 | 551,22 | 1412,51 | 215,11 |
| Итого | 1351,00 | 728,00 | 14043,33 | 39286,92 | 7236,67 | ||
| Среднее значение | 112,6 | 60,7 |
Тогда коэффициент корреляции между у и х2 составит:
Парный коэффициент корреляции между х1 и х2 рассчитывается по формуле:
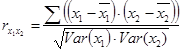
Произведем расчет необходимых параметров в таблице 4.4
Таблица 4.4
| № | х1 | х2 |  | |  |  | |
| 1 | 118,0 | 105,0 | 27,0 | 44,3 | 1197,00 | 729,00 | 1965,44 |
| 2 | 28,0 | 56,0 | -63,0 | -4,7 | 294,00 | 3969,00 | 21,78 |
| 3 | 17,0 | 54,0 | -74,0 | -6,7 | 493,33 | 5476,00 | 44,44 |
| 4 | 50,0 | 63,0 | -41,0 | 2,3 | -95,67 | 1681,00 | 5,44 |
| 5 | 56,0 | 28,0 | -35,0 | -32,7 | 1143,33 | 1225,00 | 1067,11 |
| 6 | 102,0 | 50,0 | 11,0 | -10,7 | -117,33 | 121,00 | 113,78 |
| 7 | 116,0 | 54,0 | 25,0 | -6,7 | -166,67 | 625,00 | 44,44 |
| 8 | 124,0 | 42,0 | 33,0 | -18,7 | -616,00 | 1089,00 | 348,44 |
| 9 | 114,0 | 36,0 | 23,0 | -24,7 | -567,33 | 529,00 | 608,44 |
| 10 | 154,0 | 106,0 | 63,0 | 45,3 | 2856,00 | 3969,00 | 2055,11 |
| 11 | 115,0 | 88,0 | 24,0 | 27,3 | 656,00 | 576,00 | 747,11 |
| 12 | 98,0 | 46,0 | 7,0 | -14,7 | -102,67 | 49,00 | 215,11 |
| Итого | 1092,00 | 728,00 | 4974,00 | 20038,00 | 7236,67 | ||
| Средне значение | 91,0 | 60,7 |
Тогда коэффициент корреляции между х1 и х2 составит:
При трех переменных для двухфакторного уравнения регрессии рассчитаем определители матрицы парной корреляции и межфакторной корреляции:
;
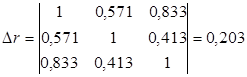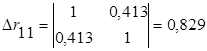
Тогда совокупный коэффициент множественной корреляции составит:
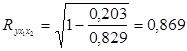
По данным из табл. 2, 3 рассчитаем теперь среднее квадратическое отклонение величин у, х1 и х2 по формулам:
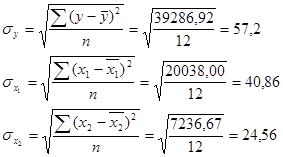
Рассчитаем теперь средние квадратические ошибки коэффициентов регрессии b1 и b2
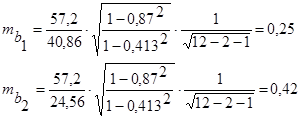
Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению значений:
При уровне значимости α = 0,05, df = 11 (n-m-1=12-2-1) степенях свободы табличное значение t-критерия Стьюдента 2,26.
Сравнив его с расчетными значениями, получаем, что 
, из чего следует, что гипотезу о несущественности параметра b2 с вероятностью 95% (p = 1 – α) следует отклонить. А вот 
из чего следует, что гипотезу о несущественности параметра b1 с вероятностью 95% (p = 1 – α) следует принять и признается статистическая незначимость параметра b1 .
2. Для характеристики относительной силы влияния х1 и х2 на у используя коэффициенты регрессии можно рассчитать средние коэффициенты эластичности. Как правило, их рассчитывают для средних значений факторов и результатов.
С увеличением среднегодовой стоимости основных фондов (х1 ) на 1% от его среднего уровня, средний объем валового дохода за год увеличится на 0,37% от своего среднего уровня; при повышении среднегодовой стоимости оборотных средств на 1% - увеличится на 0,53% от своего среднего уровня. Очевидно, что сила влияния средней стоимости оборотных средств (х2 ) на валовой доход (у) оказалась сильнее, чем сила влияния средней стоимости основных фондов (х1 ).