Контрольная работа: Экономико математические методы и модели 3
Производство
товаров
Конечный
спрос
Таблица 3.1.2
|
Первичные ресурсы | Расходы ресурса за год | ||
| цех 1 | цех 2 | цех 3 | |
| А | 180 | 30 | 50 |
| Б | 1200 | 1500 | 0 |
| В | 400 | 1200 | 300 |
| Г | 160 | 600 | 1000 |
ТРЕБУЕТСЯ:
1) найти матрицы коэффициентов прямых товаро-затрат и ресурсо-затрат на основании данных за предыдущий год;
2) найти план полных выпусков продукции каждого цеха на следующий год, обеспечивающих выполнение госзаказа по отгрузке продукции в объемах c1 =360, c2 =90, c3 =450 соответственно;
3)определить необходимый запас первичных ресурсов каждого вида.
РЕШЕНИЕ:
Если обозначить через 
полные выпуски продукции каждым цехом, то можно составить следующие соотношения
где 
– непосредственный натуральный расход продукции i -го цеха для обеспечения выпуска всей продукции j -го цеха. Числа 
называются коэффициентами прямых товаро-затрат. Их можно определить по статистическим данным за предыдущий год, т.е. 
Смысл коэффициента 
– количество продукции i -го цеха, используемое для производства 1 единицы продукции j -го цеха.
Аналогично, расход 
k -го ресурса j -м цехом представим в виде
Тогда коэффициенты 
называются коэффициен-тами прямых ресурсо-затрат. Они определяют количество k -го ресурса, необходимое для производства единицы продукции j -го цеха и находятся по результатам статистических данных за предыдущий год.
1. Для определения коэффициентов 
найдем полные выпуски продукции каждым цехом за предыдущий год хj :
x1 = 240 + 72 + 140 + 348 = 800;
x2 = 80 + 264 + 180 + 76 = 600;
x3 = 0 + 120 + 400 + 480 = 1000;
Тогда матрицы A и B коэффициентов и принимают вид:
| 240 | 72 | 140 | 0.30 | 0.12 | 0.14 |
| 800 | 600 | 1000 | |||
| 0.10 | 0.44 | 0.18 | , | ||
| A= | 80 | 264 | 180 | = | |
| 800 | 600 | 1000 | 0.00 | 0.20 | 0.40 |
| 0 | 120 | 400 | |||
| 800 | 600 | 1000 |
| 180 | 30 | 50 | 0.23 | 0.05 | 0.05 |
| 800 | 600 | 1000 | |||
| 1.50 | 2.50 | 0.00 | , | ||
| B= | 1200 | 1500 | 0 | = | |
| 800 | 600 | 1000 | 0.50 | 2.00 | 0.30 |
| 400 | 1200 | 300 | 0.20 | 1.00 | 1.00 |
| 800 | 600 | 1000 | |||
| 160 | 600 | 1000 | |||
| 800 | 600 | 1000 |
2. Заменяя выражения 
найденными коэффициентами получаем систему уравнений для определения искомых полных выпусков продукции:
 |
x1 = 0.30*x1 + 0.12*x2 + 0.14*x3 + 360, x2 = 0.10*x1 + 0.44*x2 + 0.18*x3 + 90, x3 = 0.00*x1 + 0.20*x2 + 0.40*x3 + 450. |
Эту систему можно записать в матричной форме 
где E – единичная матрица, X – матрица-столбец из неизвестных, C – матрица-столбец из чисел c1 =360, c2 =90, c3 =450. Решая полученное матричное уравнение, найдем полные выпуски продукции. Его решение имеет вид: 
Строим обратную матрицу 
Для этого найдем алгебраические дополнения 
и определитель 
для матрицы 
Имеем:
| 0,70 | -0,12 | -0,14 | ||
| ŖA= | -0,10 | 0,56 | -0,18 | , |
| 0,00 | -0,20 | 0,60 |
| 0,56 | -0,18 | ||||
| A11= | = | 0,56*0,60 – (-0,18)*(-0,20) | = | 0,30 | , |
| -0,20 | 0,60 |
Аналогично:
| -0,10 | -0,18 | -0,10 | 0,56 | ||||
| A12= – | = | 0,06 | , | A13= | = | 0,02 | , |
| 0,00 | 0,60 | 0,00 | -0,20 |
| -0,12 | -0,14 | 0,70 | -0,14 | ||||
| A21= – | = | 0,10 | , | A22= | = | 0,42 | , |
| -0,20 | 0,60 | 0,00 | 0,60 |
| 0,70 | -0,14 | -0,12 | -0,14 | ||||
| A23= – | = | 0,14 | , | A31= | = | 0,10 | , |
| -0,10 | -0,18 | 0,56 | -0,18 |
| 0,70 | -0,14 | 0,70 | -0,12 | ||||
| A32= – | = | 0,14 | , | A33= | = | 0,38 | , |
| -0,10 | -0,18 | -0,10 | 0,56 |
При этом ∆ = 0,70*0,30 – 0,12*0,06 – 0,14*0,02 = 0,20,
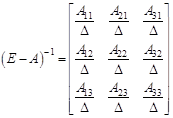 | 1,5 | 0,5 | 0,5 | |
| = | 0,3 | 2,1 | 0,7 | , |
| 0,1 | 0,7 | 1,9 |