Контрольная работа: Экономико-математический практикум
 |
|
|
|
|
|
| ||
| ||
| ||
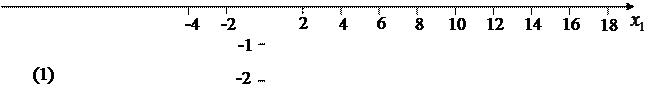
График № 1
1б) Перейдем к расширенной задаче:
Данная расширенная задача имеет начальное опорное решение 
с базисом 
. Вычисляем оценки векторов условий по базису опорного решения и значение целевой функции на опорном решении:
Расчеты проведем в таблице (Табл. 1)
Таблица 1
| 1 | -3 | 0 | 0 | 0 | 0 | M | ||||
| Б | Сб | В | А 1 | А 2 | А 3 | А 4 | А 5 | А 6 | А 7 | |
| А 3 | 0 | 9 | -2 | 3 | 1 | 0 | 0 | 0 | 0 | |
| А 4 | 0 | 53 | 5 | 2 | 0 | 1 | 0 | 0 | 0 | |
| А 5 | 0 | 17 | 4 | -7 | 0 | 0 | 1 | 0 | 0 | |
| ← | А 7 | М | 37 | 6 | 8 | 0 | 0 | 0 | 1 | 1 |
 | 0 | –1 | 3 | 0 | 0 | 0 | 0 | 0 | ||
 | 37 | 6 | 8 | 0 | 0 | 0 | 0 | 0 | ||
Начальное опорное решение не является оптимальным, так как в задаче на минимум имеются положительные оценки. Выбираем номер вектора А k , вводимого в базис опорного решения, и вектора А l , выводимого из базиса. Наибольшая положительная оценка соответствует А2 , за разрешающий элемент выбираем коэффициент 8 и выполняем преобразование Жордана.
Вектор А2 выводимый из базиса, исключаем из рассмотрения (вычеркиваем). Получаем второе опорное решение 
с базисом 
(табл. 1.3). Целевая функция 
=-3М -21. Это решение не является оптимальным, так как есть положительная оценка.
Таблица 1
| Б | Сб | B | А 1 | А 2 | А 3 | А 4 | А 5 | А 6 | |
| А2 | -3 | 3,0 | -0,7 | 1,0 | 0,3 | 0,0 | 0,0 | 0,0 | 0,0 |
| А 4 | 0 | 47,0 | 6,3 | 0,0 | -0,7 | 1,0 | 0,0 | 0,0 | 0,0 |
| А 5 | 0 | 38,0 | -0,7 | 0,0 | 2,3 | 0,0 | 1,0 | 0,0 | 0,0 |
| a7 | М | 13,0 | 11,3 | 0,0 | -2,7 | 0,0 | 0,0 | 1,0 | 1,0 |
| M+1 | -9,0 | 1,0 | 0,0 | -1,0 | 0,0 | 0,0 | 0,0 | 0,0 | |
| M+2 | 13,0 | 11,3 | 0,0 | -2,7 | 0,0 | 0,0 | 0,0 | 0,0 | |
| A2 | -3 | -2,4 | -0,6 | 1,0 | 0,0 | 0,0 | -0,1 | 0,0 | 0,0 |
| a4 | 0 | 57,9 | 6,1 | 0,0 | 0,0 | 1,0 | 0,3 | 0,0 | 0,0 |
| А 3 | 0 | 16,3 | -0,3 | 0,0 | 1,0 | 0,0 | 0,4 | 0,0 | 0,0 |
| A7 | М | 56,4 | 10,6 | 0,0 | 0,0 | 0,0 | 1,1 | 1,0 | 1,0 |
| M+1 | 7,3 | 0,7 | 0,0 | 0,0 | 0,0 | 0,4 | 0,0 | 0,0 | |
| M+2 | 56,4 | 10,6 | 0,0 | 0,0 | 0,0 | 1,1 | 0,0 | 0,0 | |
| A2 | -3 | 0,6 | 0,0 | 1,0 | 0,0 | 0,0 | -0,1 | 0,1 | 0,1 |
| a4 | 0 | 25,1 | 0,0 | 0,0 | 0,0 | 1,0 | -0,4 | -0,6 | -0,6 |
| А 5 | 0 | 17,8 | 0,0 | 0,0 | 1,0 | 0,0 | 0,5 | 0,0 | 0,0 |
| A1 | 1 | 5,3 | 1,0 | 0,0 | 0,0 | 0,0 | 0,1 | 0,1 | 0,1 |
| 3,5 | 0,0 | 0,0 | 0,0 | 0,0 | 0,4 | -0,1 | -0,1 | ||
| 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | 0,0 | -1,0 | -1,0 | ||
Целевая функция после второй итерации равна 
= 3,5. Все оценки отрицательные, план оптимален.
Оптимальный план исходной задачи Х*= (х1 * =5,3; х2 * =0,6). Минимальное значение целевой функции исходной задачи =3,5.
Ответ: minZ (X * ) =3,5.
2. Двойственная задача
Двойственная задача имеет вид.
при условиях
3. Прямая задача имеет оптимальное решение, вычислим оптимальное решение двойственной задачи, используя условия дополняющей нежесткости
Откуда следует:
