Контрольная работа: Экономико-математический практикум

Учитывая, что все переменные неотрицательны, перейдем от уравнений к неравенствам из общего решения системы.

откуда получим систему неравенств с двумя переменными

Целевую функцию выразим через свободные переменные

Окончательно получим стандартную задачу линейного программирования с двумя переменными

Строим область допустимых решений (график 2). Любая точка многоугольника удовлетворяет системе неравенств. Вершина является точкой входа семейства прямых в область решений, следовательно, в этой точке она принимает минимальное значение.

В свою очередь, =(1,32;0,12).

Решая систему уравнений получаем х₁ =2,2, х₂ =0,6. Это и будет оптимальным решением данной задачи, которому соответствует минимальное значение целевой функции Z _min

.

6

4

A

А

2

(2)

(3)

график 2

2. Решим симплекс-методом задачу линейного программирования, используя метод искусственного базиса

Составим расширенную задачу. В левые части уравнений системы ограничений вводим неотрицательные искусственные переменные с коэффициентом +1. Удобно справа от уравнений записать вводимые искусственные переменные. В первое уравнение вводим переменную х ₆ , во второе — переменную х ₇ , в третье – х₈ . Данная задача — задача на нахождение минимума. Получаем

Данная расширенная задача имеет начальное опорное решение с базисом . Вычисляем оценки векторов условий по базису опорного решения и значение целевой функции на опорном решении:

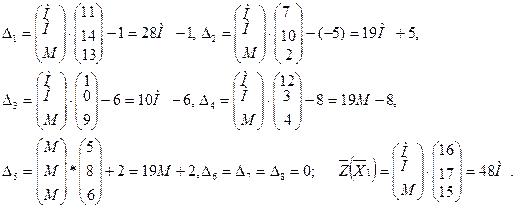
Записываем исходные и расчетные данные в симплексную таблицу (табл.2.2).

Таблица 2.2

1	-5	6	8	-2	М	M	M
Б	Сб	А 0	А 1	А 2	А 3	А 4	А 5	А 6	A7	A8
А 6	М	16	11	7	1	12	5	1	0	0
A7	M	17	14	10	0	3	8	0	1	0
←	А 8	М	15	13	2	9	4	6	0	0	1
		0	-1	5	-6	-8	2	0	0	0
		48	28	19	10	19	19	0	0	0