Контрольная работа: Экономико-математический практикум

Первое, третье и пятое ограничения выполняются как строгие неравенства, следовательно, их координаты оптимального решения исходной задачи равны нулю: . Учитывая это, первую, вторую и пятую координаты оптимального решения Х ^* находим при совместном решении уравнений-ограничений исходной задачи:

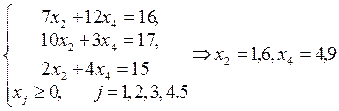
Ответ: Z (X ) = 4,2 при Х * = (0;1,6; 0;4,9;0).

Задача № 3

Транспортная задача

Ниже приведены числовые данные транспортных задач. Стоимость перевозки единицы продукции записаны в клетках таблицы. Запасы указаны справа от таблиц, а потребности – снизу. Требуется построить начальный план методами: «северо-западного угла», «минимального элемента», «двойного предпочтения», методом Фогеля. Из каждого плана найти оптимальный план методом потенциалов.

24
34	30	39	29	18	82
40	35	45	41	10	36
36	38	41	50	8	79
14	10	13	10	12	80
77	60	22	68	50

Решение.

1.Метод северо-западного угла.

Исходные данные задачи сведем в таблицу (табл. 3.1).

Таблица 3.1.

Поставщики	Потребители					Запасы
	34	30	39	29	18	82
	40	35	45	41	10	36
	36	38	41	50	8	79
	14	10	13	10	12	8 0
Потребности	77	60	22	6 8	50

Решение. Построим опорный план задачи методом северо-западного угла.

Объем перевозки и последовательность заполнения матрицы будем записывать в соответствующие клетки табл. 3.2.

Цифры, стоящие в скобках над объемами перевозок, обозначают номер шага, на котором определяются эти перевозки.

1. х₁₁ ⁽¹⁾ =min(82,77)=77. Потребности первого потребителя удовлетворены, исключаем его. Запасы первого поставщика уменьшились на х₁₁ ⁽¹⁾ и стали равны (82-77=5) 5.

2. х₁₂ ⁽¹⁾ =min(5,60)=5. Запасы первого поставщика исчерпаны, исключим первую строку. Второй потребитель удовлетворил свои потребности на 5 единиц, его спрос уменьшился на величину х₁₁ ⁽¹⁾ и стал равным 55.

3. х₂₂ ⁽³⁾ =min(36,55)=36. После третьего шага ресурсы поставщика А₂ исчерпаны. Спрос потребителя B₂ равен b₂ ⁽³⁾ =55-36=19.

4. х₂₃ ⁽⁴⁾ =min(79,19)=19. Следует исключить потребителя B_2. Ресурсы поставщика А₃ ⁽⁴⁾ = a₃ – х₂₃ ⁽⁴⁾ =79-19=60 составляет 60 единиц.

5. х₃₃ ⁽⁵⁾ =min(60,22)=22. Потребитель В₃ полностью удовлетворил свой спрос, исключаем столбец 3.

6. х₃₄ ⁽⁶⁾ =min(38,68)=38. Следует исключить поставщика А₃ , запасы которого исчерпаны. Спрос потребителя В₄ в₄ ⁽⁶⁾ – х₃₄ ⁽⁵⁾ =68-38=30 составляет 30 единиц.

7. х₄₄ ⁽⁷⁾ =min(80,30)=30. Спрос четвертого потребителя удовлетворен. Запасы поставщика А₄ составляет

80-30=50.

8. х₄₅ ⁽⁸⁾ =min(50,50)=0. Запасы исчерпаны, потребности удовлетворены.

Опорный план построен (табл. 3.2).

Таблица 3.2.

34	3 0	3 9	29	18
77(1)	5(2)	82
4 0	35	4 5	41	10
36(3)	36
36	3 8	41	50	8
19(4 )	22(5)	38(6)	79
1 4	1 0	1 3	1 0	1 2
30(7)	50( 8 )	8 0
7 7	60	22	6 8	50

Суммарные транспортные издержки на перевозку продукции от поставщиков к потребителю составляют

2.Метод минимального элемента.

Исходные данные

поставщики	потребители					Запасы
	В1	В2	В3	В4	В5
А1	34	30	39	29	18	82
А2	40	35	45	41	10	36
А3	36	38	41	50	8	79
А4	14	10	13	10	12	8 0
потребности	77	60	22	6 8	50

1. Объем запасов и потребностей после первого шага уменьшается на величину: х₃₁ ⁽¹⁾ =50; . Запасы пятого поставщика исчерпаны, потребности первого потребителя уменьшились на 50 единиц и стали равны 29, исключаем пятый столбец.