Контрольная работа: Экономико-математическое моделирование анализа ресурсов

Для определения направления движения к оптиму построим вектор – градиента Їс (с₁ ;с₂ ), координаты которого являются частными производными целевой функции, т. е. с (3;4).

Построим линию уровня l_0, приравняем целевую функцию к 0

3х₁ +4х₂ =0

Х1	0	-4
Х2	0	0

Передвигая линию уровня l0 в направлении обратном направлению вектора – градиента, т. к задача на минимум, достигнем минимальную точку целевой функции. Найдем координаты этой точки, решая систему из двух уравнений прямых, дающих в пересечении точку минимума:

(.) А = l₁ ∩l₃

3х₁ +2х₂ =10, *3 «-»

4х₁ +6х₂ =20

5х₁ =10

х₁ =2

Подставим в первое уравнение 3*2+2х₂ =10,

2х₂ =10-6,

2х₂ =4,

х₂ =2.

Fmin=3*2+4*2=6+8=14 ден. ед.

График:

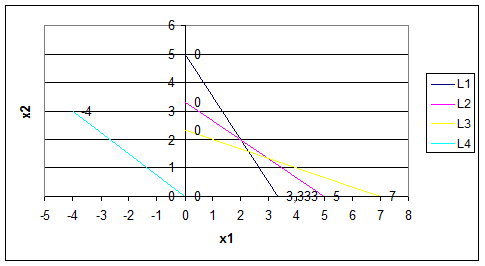
Ответ: чтобы обеспечить эффективное питание почвы при минимизированной стоимости, которая составила 14 ден ед, необходимо купить 2 набора обычного удобрения и 2 набора улучшенного. Если данную задачу решать на максимум, то задача не имеет решения, так как целевая функция не ограничена сверху, т. е Fmax=+∞

2. Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.

тип сырья	норма расхода сырья на одно изделие				запасы сырья
	А	Б	« 1 2 3 4 5 6 7 8 9 10 » К-во Просмотров: 542 Бесплатно скачать Контрольная работа: Экономико-математическое моделирование анализа ресурсов >>> Скачать <<< Меню Поиск