(30)

т.е. результат, как и следовало, получился тот же.

Для двух параллельных проводников, расположенных с любым сдвигом, Г.Б. Холявский получил удобную для расчета коэффициента контура формулу, основанную на геометрической интерпретации приведенных выше уравнений.

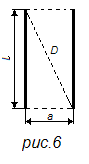
Величина представляет собой длину диагонали D (рис. 6) прямоугольника со сторонами l и а; следовательно, согласно уравнению (20) для проводников равной длины

(31a)

а согласно уравнению (25) для проводников неравной длины (рис. 7)

(31б)

т.е. коэффициент контура равен разности суммарных диагоналей и боковых сторон четырехугольника (прямоугольник, трапеция, параллелограмм), построенного на данных отрезках проводников, деленной на его высоту.

Для проводников прямоугольного сечения (шин) следует вводить поправочный коэффициент — коэффициент формы k _ф , зависящий от размеров проводников и расстояний между ними:

(32)

4. Электродинамические силы между взаимно перпендикулярными проводниками

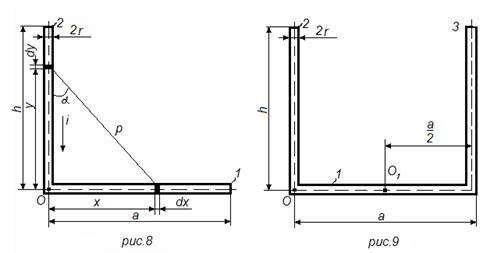
На рис. 8 и 9 приведены часто встречающиеся в аппаратах формы перпендикулярно расположенных проводников, например в рубильниках, мостиковых контактных системах и многих других аппаратах и узлах. Произведя расчеты, аналогичные предыдущим (первый метод), получим следующие выражения для сил, действующих на проводник 1 по рис.8
при h →∞

(33)

и при h конечном

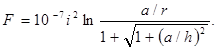(34)

по рис. 9 сила будет соответственно в два раза большей:

(35)

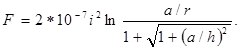(36)

Моменты относительно точки О, действующие на проводник 1 ( h →∞), по рис. 8:

(37)

(38)

Момент относительно точки О , действующий на половину проводника 1 (рис. 9),

(39)

5. Электродинамические силы в кольцевом витке и между кольцевыми витками

Для одного витка

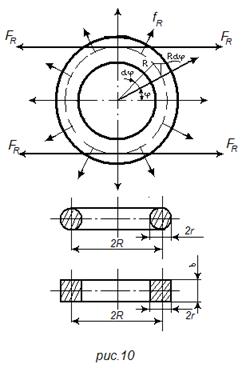
В кольцевом витке (рис. 10) с током i возникают радиальные силы f_R , стремящиеся увеличить его периметр, т.е. разорвать виток. Если считать, что сечение проводника не деформируется, то согласно выражению (13) общая радиальная сила, действующая на виток, будет

(40)