Контрольная работа: Элементы теории вероятностей. Случайные события

D – хотя бы одно попадание, т.е. или одно попадание, или два попадания или три попадания

Р(D) = Р( ₁ и ₂ и А₃ или ₁ и А ₂ и ₃ или А₁ и ₂ и ₃ ИЛИ ₁ и А₂ и А₃ или А₁ и ₂ и А₃ или А₁ и ₂ и А₃ ИЛИ А₁ и А₂ и А₃ )

или по формуле

Р(D) = 1 – Р( ₁ и ₂ и ₃ )

Е – больше одного попадания, т.е. или два попадания или три попадания

Р(Е) = Р( ₁ и А₂ и А₃ или А₁ и ₂ и А₃ или А₁ и ₂ и А₃ или А₁ и А₂ и А₃ )

F – не больше одного попадания, т.е. одно попадание и два промаха

Р(F) = Р( ₁ и ₂ и А₃ или ₁ и А ₂ и ₃ или А₁ и ₂ и ₃ )

Задача 3.

Игральный кубик бросают два раза. Описать пространство элементарных событий. Описать события: А – сумма появившихся очков равна 8; В – по крайней мере один раз появится 6.

Решение:

Будем считать пространством элементарных событий множество пар чисел (i , j ), где i (соответственно j ) есть число очков, выпавших при первом (втором) подбрасывании, тогда множество элементарных событий будет таким:

W={(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)}

А – сумма появившихся очков равна 8. Этому событию благоприятствуют такие элементарные события А={(2,6) (6,2) (5,3) (3,5) (4,4)}.

В – по крайней мере один раз появится 6. Этому событию благоприятствуют такие элементарные события В={(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) (1,6) (2,6) (3,6) (4,6) (5,6)}.

Задача 4.

В вазе с цветами 15 гвоздик: 5 белых и 10 красных. Из вазы наугад вынимают 2 цветка. Какова вероятность того, что эти цветки: а) оба белые; б) оба красные; в) разного цвета; г) одного цвета.

Решение:

а) Пусть событие А состоит в том, что оба вынутых из вазы цветка белые.

Количество возможных способов взять 2 цветка из 15-ти равно , т.е. = 7×15 = 105, а количество возможных способов взять 2 белых цветка из 5-ти белых равно = 2×5 = 10. Тогда по классическому определению вероятность события А равна

.

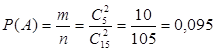б) Пусть событие В состоит в том, что оба вынутых из вазы цветка красные.

Количество возможных способов взять 2 цветка из 15-ти равно , т.е. = 7×15 = 105, а количество возможных способов взять 2 красных цветка из 10-ти красных равно = 9×5 = 45. Тогда по классическому определению вероятность события В равна

.