Контрольная работа: Явление резонанса и электрических цепей

Выполнил:

Антропов А. И.

Проверила:

Бородина А. В.

Самара 2009

Электрические цепи переменного тока. Явление резонанса

Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением .

Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z ]=0 или Im[Y ]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.

Для определения условий возникновения режима резонанса в электрической цепи нужно:

· найти ее комплексное сопротивление или проводимость;

· выделить мнимую часть и приравнять нулю.

Все параметры электрической цепи, входящие в полученное уравнение, будут в той или иной степени влиять на характеристики явления резонанса.

Уравнение Im[Z ]=0 может иметь несколько корней решения относительно какого-либо параметра. Это означает возможность возникновения резонанса при всех значениях этого параметра, соответствующих корням решения и имеющих физический смысл.

В электрических цепях резонанс может рассматриваться в задачах:

· анализа этого явления при вариации параметров цепи;

· синтеза цепи с заданными резонансными параметрами.

Электрические цепи с большим количеством реактивных элементов и связей могут представлять значительную сложность при анализе и почти никогда не используются для синтеза цепей с заданными свойствами, т.к. для них не всегда возможно получить однозначное решение. Поэтому на практике исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с требуемыми параметрами.

Сдвиг фаз между током и напряжением. Понятие двухполюсника

Простейшими электрическими цепями, в которых может возникать резонанс, являются последовательное и параллельное соединения резистора, индуктивности и емкости. Соответственно схеме соединения, эти цепи называются последовательным и параллельным резонансным контуром . Наличие резистивного сопротивления в резонансном контуре по определению не является обязательным и оно может отсутствовать как отдельный элемент (резистор). Однако при анализе резистивным сопротивлением следует учитывать по крайней мере сопротивления проводников.

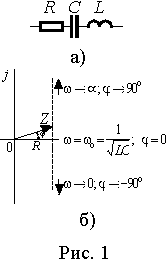
Последовательный резонансный контур представлен на рис. 1 а). Комплексное сопротивление цепи равно

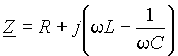
Условием резонанса из выражения (1) будет

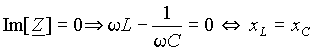
Таким образом, резонанс в цепи наступает независимо от значения резистивного сопротивления R когда индуктивное сопротивление x_L = wL равно емкостному x_C = 1/(wC ) . Как следует из выражения (2), это состояние может быть получено вариацией любого их трех параметров - L , C и w , а также любой их комбинацией. При вариации одного из параметров условие резонанса можно представить в виде

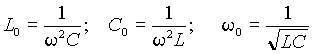
Все величины, входящие в выражение (3) положительны, поэтому эти условия выполнимы всегда, т.е. резонанс в последовательном контуре можно создать

· изменением индуктивности L при постоянных значениях C и w ;

· изменением емкости C при постоянных значениях L и w ;

--> ЧИТАТЬ ПОЛНОСТЬЮ <--