Контрольная работа: Явление резонанса и электрических цепей

Наибольший интерес для практики представляет вариация частоты. Поэтому рассмотрим процессы в контуре при этом условии.

При изменении частоты резистивная составляющая комплексного сопротивления цепи Z остается постоянной, а реактивная изменяется. Поэтому конец вектора Z на комплексной плоскости перемещается по прямой параллельной мнимой оси и проходящей через точку R вещественной оси (рис. 1 б)). В режиме резонанса мнимая составляющая Z равна нулю и Z = Z = Z _min = R , j = 0 , т.е. полное сопротивление при резонансе соответствует минимальному значению .

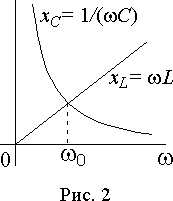
Индуктивное и емкостное сопротивления изменяются в зависимости от частоты так, как показано на рис. 2. При частоте стремящейся к нулю x_C ®µ , x_L ® 0 , и j® - 90° (рис. 1 б)). При бесконечном увеличении частоты - x_L ®µ , x_C ® 0 , а j® 90° . Равенство сопротивлений x_L и x_C наступает в режиме резонанса при частоте w₀ .

Рассмотрим теперь падения напряжения на элементах контура. Пусть резонансный контур питается от источника, обладающего свойствами источника ЭДС, т.е. напряжение на входе контура u = const, и пусть ток в контуре равен i =I_m sinwt . Падение напряжения на входе уравновешивается суммой напряжений на элементах

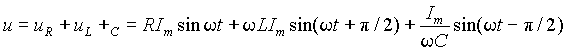
Переходя от амплитудных значений к действующим, из выражения (4) получим напряжения на отдельных элементах контура

а при резонансной частоте

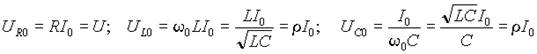
где

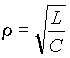
величина, имеющая размерность сопротивления и называемая волновым или характеристическим сопротивлением контура.

Следовательно, при резонансе

· напряжение на резисторе равно напряжению на входе контура;

· напряжения на реактивных элементах одинаковы и пропорциональны волновому сопротивлению контура;

· соотношение напряжения на входе контура (на резисторе) и напряжений на реактивных элементах определяется соотношением резистивного и волнового сопротивлений.

Отношение волнового сопротивления к резистивному r /R = Q , называется добротностью контура , а величина обратная D =1/Q - затуханием . Таким образом, добротность числено равна отношению напряжения на реактивном элементе контура к напряжению на резисторе или на входе в режиме резонанса. Добротность может составлять несколько десятков единиц и во столько же раз напряжение на реактивных элементах контура будет превышать входное. Поэтому резонанс в последовательном контуре называется резонансом напряжений .

Рассмотрим зависимости напряжений и тока в контуре от частоты. Для возможности обобщенного анализа перейдем в выражениях (5) к относительным единицам, разделив их на входное напряжение при резонансе

U =RI ₀

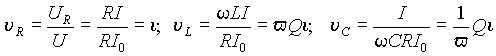
где i =I /I ₀ , u_k =U_k /U , v = w /w₀ - соответственно ток, напряжение и частота в относительных единицах, в которых в качестве базовых величин приняты ток I ₀ , напряжение на входе U и частота w₀ в режиме резонанса.

Абсолютный и относительный ток в контуре равен

Из выражений (7) и (8) следует, что характер изменения всех величин при изменении частоты зависит только от добротности контура. Графическое представление их при Q =2 приведено на рис. 3 в логарифмическом (а) и линейном (б) масштабах оси абсцисс.

На рис. 3 кривые A (v), B (v) и C (v) соответствуют напряжению на индуктивности, емкости и резисторе или току в контуре. Кривые A (v)=u_L (v) и B (v)=u_C (v) имеют максимумы, напряжения в которых определяются выражением

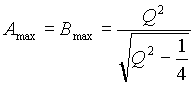, (9)

а относительные частоты максимумов равны