Контрольная работа: Явление резонанса и электрических цепей

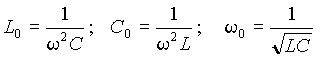
При изменении частоты питания изменяется только мнимая составляющая вектора комплексной проводимости Y , поэтому его конец перемещается на комплексной плоскости по прямой параллельной мнимой оси и проходящей через точку G =1/R , соответствующую вещественной составляющей проводимости (рис. 8 б)). При частоте резонанса модуль вектора минимален, а при стремлении частоты к нулю и бесконечности, его значение стремится к бесконечности. При этом угол сдвига фаз между током и напряжением j на входе контура стремится к 90° при w® 0 и к - 90° при w®µ .

Для параллельного соединения токи в отдельных элементах можно представить через проводимости и общее падение напряжения U в виде

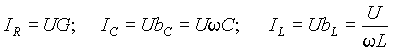
Пусть в режиме резонанса падение напряжения на входе контура равно U ₀ , тогда токи в отдельных элементах будут

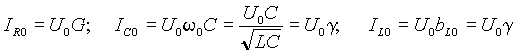
где

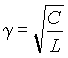
волновая или характеристическая проводимость контура. Как следует из выражений (17), при резонансе токи в реактивных элементах одинаковы, а входной ток равен току в резисторе R . Отношение Q =g /G называется добротностью, а величина обратная D =1/Q - затуханием параллельного резонансного контура. Таким образом, добротность равна отношению токов в реактивных элементах контура к току на входе или в резисторе. В электрических цепях добротность может достигать значений в несколько десятков единиц и во столько же раз токи в индуктивности и емкости будут превышать входной ток. Поэтому резонанс в параллельном контуре называется резонансом токов .

Падение напряжения на входе контура U при питании его от источника, обладающего свойствами источника тока и формирующего ток с действующим значением I , будет равно

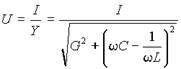
Отсюда, напряжение на входе в режиме резонанса U ₀ = I /G . Тогда ток в контуре - I =U ₀ G . Перейдем к относительным единицам в выражениях (16) и (18), приняв в качестве базовых значений напряжение на входе при резонансе и ток контура, выраженный через это напряжение. Тогда получим

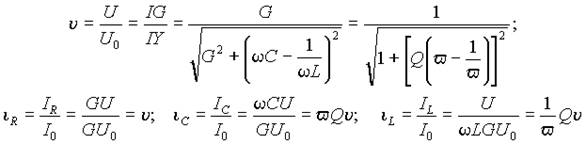
Выражения (18) полностью совпадают с выражениями (7) и (8) для частотных характеристик последовательного контура, если в них относительные токи и напряжения поменять местами. Следовательно, характеристики рис. 3 будут связаны с выражениями (18) следующим образом: A (v)=i_С (v); B (v)=i_L (v) и C (v)=i_R (v)=u (v ). Для относительных токов i_С , i_L и i_R справедливыми будут также все закономерности отмеченные для относительных напряжений последовательного контура.

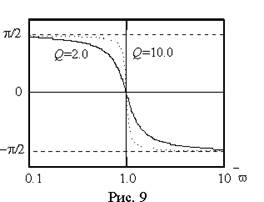
Из выражения (14) рассмотренную выше качественно фазовую частотную характеристику можно представить аналитически в виде

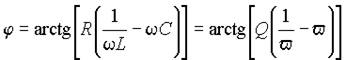
т.е. она совпадает с характеристикой последовательного контура, но имеет противоположный знак.

Допустим теперь, что параллельный контур питается от источника со свойствами источника ЭДС. В режиме резонанса входной ток также будет равен току через резистор

I ₀ =U /R =UG.

Соотнесем все выражения (16) с этим током, приняв его за базовую величину. Тогда

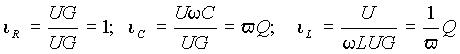
Относительный входной ток i можно определить, пользуясь тем, что в треугольнике токов он является гипотенузой

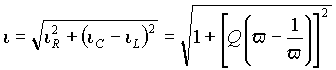
Выражения (19) и (20) для относительных токов совпадают с выражениями (12) и (13) для относительных напряжений последовательного контура. Следовательно, на рис. 7 - i_C (v )=A (v ), i_L (v )=B (v ) и i_R (v )= i (v )=C (v ).

Сравнивая частотные характеристики при питании параллельного резонансного контура от источника тока с характеристиками при питании его от источника ЭДС, можно сделать выводы аналогичные тем, которые были сделаны для последовательного контура:

· частотные характеристики токов и напряжения контура принципиально отличаются друг от друга, т.к. при питании от источника тока сумма токов остается постоянной и происходит только их перераспределение между элементами, а при питании от источника ЭДС токи в каждом элементе формируются независимо;

· режимы резонанса для обоих случаев полностью идентичны;

· фазовые частотные характеристики для обоих случаев также идентичны .