Контрольная работа: Явление резонанса и электрических цепей

Параллельный резонансный контур может содержать резистивные сопротивления (рис. 10). В этом случае комплексные проводимости ветвей будут равны

Y ₁ =G ₁ +jB ₁ ; Y ₂ =G ₂ +jB ₁ ,

а общая проводимость

Y = Y ₁ + Y ₂ = G ₁ +G ₂ +j (B ₁ +B ₂ ).

Условием резонанса будет:

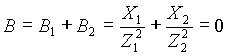
Раскрывая выражение (23) через параметры цепи, получим

,

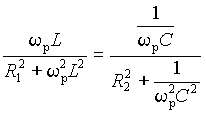откуда резонансная частота w_р –

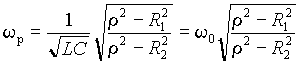
где

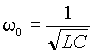
резонансная частота в простейшем параллельном контуре (рис. 8 а)), а

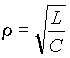
волновое сопротивление простейшего параллельного контура.

Анализ выражения (21) показывает, что при разных резистивных сопротивлениях R ₁ ¹R ₂ резонанс возможен только, если оба сопротивления одновременно больше или меньше r . В противном случае выражение под корнем отрицательно, резонансная частота мнимая и не имеет физического смысла.

Если R ₁ = R ₂ , то w_р = w₀ , т.е. резонанс наступает при той же частоте, что и в простейшем контуре без потерь (рис. 8 а)).

Однако при этом условии возможен вариант, когда R ₁ = R ₂ = r . В этом случае подкоренное выражение в (21) становится неопределенным (0/0) и требуется его дополнительный анализ.

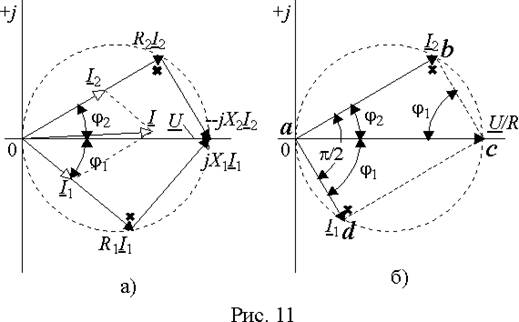
Ветви контура соединены параллельно и общее падение напряжения на них одинаково и равно сумме падений напряжения на элементах ветви. При любых изменениях частоты угол между напряжением на резисторе и реактивном элементе составляет 90° и т.к. сумма их постоянна и равна входному напряжению, то геометрическим местом точек конца вектора падения напряжения на резисторе будет полуокружность (рис. 11 а)). Причем, векторы ветви с индуктивностью будут вписываться в нижнюю полуокружность, а ветви с емкостью - в верхнюю. Входной ток I равен сумме токов ветвей I ₁ и I ₂ и резонанс наступает, если его направление совпадает с вектором входного напряжения U .

Разделим комплексные числа, соответствующие векторам напряжений рис. 11 а), на R = R ₁ = R ₂ = r и построим векторную диаграмму токов для режима резонанса (рис. 11 б)), т.е. так, чтобы сумма векторов I ₁ и I ₂ была равна U/R . Параллелограмм abcd имеет два противоположных прямых угла, поэтому два других угла j₁ + j₂ = p /2 . То, что сумма углов j₁ и j₂ равна 90° доказывается также и тем, что

.

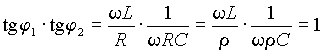Таким образом, при любой частоте векторы токов I ₁ и I ₂ образуют прямоугольник, вершины которого расположены на окружности, а диагональю является вектор U/R . Отсюда следует, что при всех частотах входной ток одинаков, совпадает по направлению с напряжением и полное сопротивление цепи чисто резистивное и равно r .