Контрольная работа: Кинематическое исследование кривошипно-балансирного механизма
.
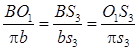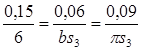откуда bS 3 =2,4
πS 3 = bS 3 - абсолютное ускорение точки S 3 .
Угловое ускорение относительно вращательного движения равно:
.
Кинетостатический анализ механизма
Определим давление во всех кинематических парах и уравновешивающую силу, приложенную к шарниру А кривошипа кривошипно-балансирного механизма.
Решение:
1. Строим планы скоростей и ускорений механизма
2. Определяем силы инерции и моменты сил инерции для звеньев механизма. Знак минус показывает, что направление силы или момента сил противоположно ускорению.
Звено АВ совершает плоскопараллельное движение, и действие сил инерции для него сводится к силе и моменту сил инерции:
Р и2 = -J 2/ q · as=-50/100*2,875=-1,44 ;
М и2 = -Js · εВА = -Js · (аВА / lАВ ) =-0,45.
Сила Р и2 направлена в сторону, противоположную направлению ускорения а s 2 . Момент инерции М и2 - в сторону, противоположную направлению углового ускорения εВА , а εВА направлено в ту же сторону, что и касательное ускорение аВА .
Заменим силу инерции Р и2 и момент сил инерции М и2 , действующие на шатун АВ , одной результирующей силой.
Для этого момент инерции М и2 заменяем парой сил, где в качестве силы пары берем силу, равную Р и2 . Одну из сил пары прикладываем к центру тяжести и направляем ее по линии действия Р и2 в противоположную сторону.
Определяем плечо силы из соотношения:
М и2 = Р и2 · h
h = М и2 /Р и2 = М и2 /Р и2 =0,3, так как Р и2 = Р и2 .
Звено В (ползун) совершает поступательное движение, поэтому действует только сила инерции
Р и3 = -mAB = - (J 3 /g ) · aB . =-0,66
3. Определяем силы давления в кинематических парах (рис. 16):
а) для определения сил давления в кинематической паре 3-4 выделим группу Ассура и рассмотрим ее равновесие.
Поскольку группа отсоединена от механизма, действие отброшенных частей последнего звена группы нужно заменить силами. Как действуют эти силы, пока не известно, поэтому изображаем их произвольно. Вектор Q 1-2 - сила действия звена 1 на звено 2, вектор Q 4-3 -сила действия звена 4 на звено 3.
Согласно принципу Д’Аламбера, анализируемая группа находится в состоянии равновесия. Можно к ней применить уравнение и определить неизвестные силы.
ΣР i = Р и2 + J 2 + Р и3 + Р сопр + J 3 + Q 1-2 + Q 4-3 = 0
Так как группа Ассура находится в равновесии, то алгебраическая сумма моментов всех сил относительно А равна нулю.
ΣМА = Р и2 · h 1 - J 2 · h 2 + Q 4-3 · h 3 - J 3 · h 3 + (Р и3 + Р сопр ) · h 4 = 0
Из этого уравнения выразим Q 4-3 :
