Контрольная работа: Классический метод расчета переходных процессов в линейных цепях

,

.

6) расчет произвольных постоянных

В нашем случае:

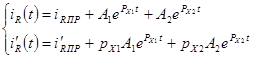
При :

Тогда из (1)

Из (3)(2)

Ответ: , А.

3. Особенности переходных процессов в цепях с одним реактивным элементом

В таких цепях характеристическое уравнение будет первого порядка. Получить это уравнение можно, например, так:

По способу Zвх(p)=0, при этом схемы могут иметь вид:

Рис (1) , ,

Рис (2) , .

Видно, что корень характеристического уравнения получается отрицательным, т.е. с течением времени свободная составляющая .

Ясно, что в разных схемах различными получаются величина А, величина , но свободная составляющая всегда будет иметь вид затухающей экспоненты. Для таких функций вводятся специальная характеристика.

Постоянная времени цепи (τ) – есть интервал времени, за который амплитуда свободной составляющей уменьшается в e раз.

Воспользовавшись этим определением, можно найти τ таким образом так как , то

.

В цепи: ,

т.е. τ зависит только от параметров рассматриваемой цепи (τ не зависит от начальных условий и напряжений источника).

Используя понятие τ, можно условно ввести понятие длительности переходного процесса. Так как , то

t	τ	3τ	5τ
	0,36	0,05	0,004

В соответствие с этой таблицей принимают, что переходный процесс длится . К концу этого времени график переходного процесса практически сливается с принужденной составляющей.

Если известен график переходного процесса, из него можно найти τ.

Проще всего сделать так: на глаз определить, где кончается переходный процесс.