Контрольная работа: Классический метод расчета переходных процессов в линейных цепях

В зависимости от величины подкоренного выражения получаются разные типы корней.

Если , то подкоренное выражение равно нулю, и следовательно получим . Из выражения (*) видно, что это получается при некотором «критическом» значении сопротивления .

Если же R > R_кр то подкоренное выражение положительно, и получим два вещественных различных корня. Если R < R_кр , под корнем будет отрицательное число, и получим пару комплексно сопряжённых корней.

1) R > R_кр (два вещественных различных корня) и тогда решение для тока запишется в виде:

,

,

и при t = 0 получаем два уравнения для расчёта произвольных постоянных:

Из (1): , и подставляя в (2):

График проще построить по частям (принуждённая составляющая и каждое слагаемое свободной составляющей, а затем сложить).

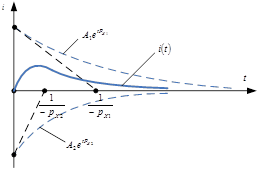
Говорят, что это апериодический процесс.

Аналогично можно получить выражения и графики для напряжения на электродах:

2) R = R_кр

,

при

Графики имеют в этом случае точно такой же вид, как и в предыдущем случае, но в первом случае процессы идут медленнее, чем во втором. Этот случай называется критическим переходным процессом.

3) R < R_кр

, ,

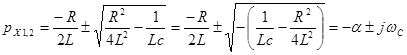
т.е. при α→ 0 ω_c стремится к резонансной частоте данной цепи.

Решение запишется в виде:

(классический метод)