Контрольная работа: Коэффициент детерминации. Значимость уравнения регрессии

Промежуточные расчеты представим в таблице:

Таблица 5. Промежуточные вычисления для расчета t- критерия

xi
38	6,25
28	56,25
27	72,25
37	2,25
46	110,25
27	72,25
41	30,25
39	12,25
28	56,25
44	72,25

=490,50

для уровня значимости 0,05 и числа степеней свободы n-2=8

Так как и можно сделать вывод, что оба коэффициента регрессии значимые.

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

Коэффициент детерминации определяется по формуле:

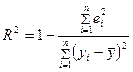
Из расчетов нам известно, что

; .

Рассчитаем :

Таблица 6. Промежуточные вычисления для расчета коэффициента детерминации.

69	9,6	92,16
52	-7,4	54,76
46	-13,4	179,56
63	3,6	12,96
73	13,6	184,96
48	-11,4	129,96
67	7,6	57,76
62	2,6	6,76
47	-12,4	153,76
67	7,6	57,76

=930,4

=0,917.

Т.к. значение коэффициента детерминации близко к единице, качество модели считается высоким.

Теперь проверим значимость уравнения регрессии. Рассчитаем значение F-критерия Фишера по формуле:

Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. >.

Средняя относительная ошибка аппроксимации находится по формуле:

Таблица 7. Промежуточные вычисления для расчета средней относительной ошибки аппроксимации.

yi
69	6,305	0,091377
52	2,495	0,047981
46	-2,186	0,047522
63	1,624	0,025778
73	-0,247	0,003384
48	-0,186	0,003875
67	0,348	0,005194
62	-2,014	0,032484
47	-2,505	0,053298
67	-3,609	0,053866

,

значит модель имеет хорошее качество.