Контрольная работа: Конечно-разностный метод решения для уравнений параболического типа
Сетка может состоять из клеток разной конфигурации: квадратных, прямоугольных, треугольных и других. После построения сетки исходное дифференциальное уравнение заменяется разностным уравнением во всех внутренних узлах сетки. Затем на основании граничных условий устанавливаются значения искомого решения в граничных узлах. Присоединяя граничные условия сеточной задачи к разностным уравнениям, записанных для внутренних узлов, получаем систему уравнений, из которой определяем значения искомого решения во всех узлах сетки.
Нанесем на пространственно-временную область 
, 
конечно разностную сетку ωh,τ :
(10)
с пространственным шагом h = l / N и шагом по времени τ=T/K.
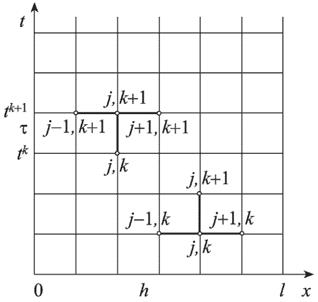
Рисунок 1 – Конечно-разностная сетка
Введем два временных слоя : нижний 
,на котором распределение искомой функции u ( xj , tk ) , 
, известно (при к = 0 распределение определяется начальным условием (4)u ( xj , tk )=ψ( xj ) ), и верхний временной слой tk +1 =( k +1) τ , на котором распределение искомой функции u ( xj , tk +1 ) , .
Сеточной функцией задачи (1)-(4) называют однозначное отображение целых аргументов j , k в значения функции 
.
На введенной сетке вводят сеточные функции 
, 
первая из которых известна, вторая подлежит определению. Для определения в задаче (1)-(4) заменяют (аппроксимируют) дифференциальные операторы отношением конечных разностей (более подробно это рассматривают в разделах численных методов «Численное дифференцирование»), получают
, (11)
, (12)
Подставляя (11), (12) в задачу (1)-(4), получим явную конечно-разностную схему для этой задачи в форме
(13)
В каждом уравнении этой задачи все значения сеточной функции известны, за исключением одного, 
, которое может быть определено явно из соотношений (13). В соотношения (13) краевые условия входят при значениях j =1 и j = N - l , a начальное условие – при k = 0.
Если в (12) дифференциальный оператор по пространственной переменной аппроксимировать отношением конечных разностей на верхнем временном слое:
, (14)
то после подстановки (11), (14) в задачу (1)-(4) получим неявную конечно-разностную схему для этой задачи:
(15)
Теперь сеточную функцию
на верхнем временном слое можно получить из решения (15) с трехдиагональной матрицей. Эта СЛАУ в форме, пригодной для использования метода прогонки, имеет вид
где
;
;
, ;
;
;
;
.
Шаблоном конечно-разностной схемы называют ее геометрическую интерпретацию на конечно-разностной сетке. На рисунке приведены шаблоны для явной и неявной конечно-разностных схем при аппроксимации задачи.