Контрольная работа: Конечно-разностный метод решения для уравнений параболического типа
В этом выражении дифференциальный оператор 
от квадратной скобки в соответствии с дифференциальным уравнением равен дифференциальному оператору 
, в соответствии с чем вышеприведенное равенство приобретает вид
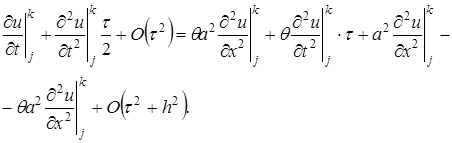
После упрощения получаем
,
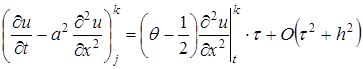откуда видно, что для схемы Кранка-Николсона (θ = 1/2) порядок аппроксимации схемы (23) составляет 
, т.е. на один порядок по времени выше, чем для обычных явных или неявных схем. Таким образом, схема Кранка-Николсона при θ = 1/2 абсолютно устойчива и имеет второй порядок аппроксимации по времени и пространственной переменной х .
Используем в уравнение (23) подстановку r= a2 k / h2 . Но в то же время его нужно решить для трех "еще не вычисленных" значений 
, 
, и 
. Это возможно, если все значения перенести в левую часть уравнения. Затем упорядочим члены уравнения (23) и в результате получим неявную разностную формулу
(26)
для i=2,3,…, n-1 . Члены в правой части формулы (26) известны. Таким образом, формула (26) имеет вид линейной трехдиагональной системы АХ=В. Шесть точек, используемых в формуле Кранка-Николсона (26), вместе с промежуточной точкой решетки, на которой основаны численные приближения, показаны на рисунке 5.
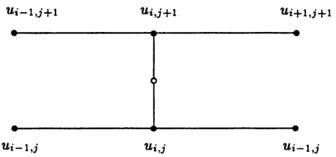
Рисунок 5 – Шаблон (схема) метода Кранка-Николсона
Иногда в формуле (26) используется значение r=1 . В этом случае приращение по оси t равно 
, формула (26) упрощается и принимает вид
, (27)
для i=2,3,…, n-1 . Граничные условия используются в первом и последнем уравнениях (т. е. в 
и 
соответственно).
Уравнения (27) особенно привлекательны при записи в форме трехдиагональной матрицы АХ = В.
Если метод Кранка-Николсона реализуется на компьютере, то линейную систему АХ = В можно решить либо прямым методом, либо итерационным.
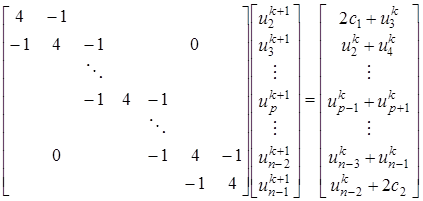
2. Практическая часть
2.1 Постановка задачи
Используем метод Кранка-Николсона, чтобы решить уравнение
,
где x ϵ(0;1),
t ϵ(0;0.1),
с начальным условием
,
где t=0,
x ϵ(0;1),
и граничными условиями
u(0,t) = g1 (t) ≡ 0,