Математика / Контрольная работа: Конечно-разностный метод решения для уравнений параболического типа

Контрольная работа: Конечно-разностный метод решения для уравнений параболического типа

2.2 Решение в ППП MatLab

Решение будем искать в ППП MatLab 7. Создадим четыре выполняемых m-фала: crnich.m – файл-функция с реализацией метода Кранка-Николсона; trisys.m – файл-функция метода прогонки; f.m – файл-функция задающая начальное условие задачи; fе.m – файл-функция задающая функцию определяющую точное решение задачи(найдена аналитическим путем). Листинги программ представлены в приложении А.

Для простоты возьмем шаг Δх = h = 0,1 и Δ t = к = 0,01 . Таким образом, соотношение r =1. Пусть решетка имеет n=11 столбцов в ширину и m=11 рядов в высоту.

2.3 Анализ результатов

Решения для данных параметров отразим в таблице 1. Трехмерное изображение данных из таблицы покажем на рисунке 5.

Таблица 1 – Значения u(х i , ti ), полученные методом Кранка-Николсона

xi 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
ti
0 0 1.1180 1.5388 1.1180 0.3633 0 0.3633 1.1180 1.5388 1.1180 0
0.01 0 0.6169 0.9288 0.8621 0.6177 0.4905 0.6177 0.8621 0.9288 0.6169 0
0.02 0 0.3942 0.6480 0.7186 0.6800 0.6488 0.6800 0.7186 0.6480 0.3942 0
0.03 0 0.2887 0.5067 0.6253 0.6665 0.6733 0.6665 0.6253 0.5067 0.2887 0
0.04 0 0.2331 0.4258 0.5560 0.6251 0.6458 0.6251 0.5560 0.4258 0.2331 0
0.05 0 0.1995 0.3720 0.4996 0.5754 0.6002 0.5754 0.4996 0.3720 0.1995 0
0.06 0 0.1759 0.3315 0.4511 0.5253 0.5504 0.5253 0.4511 0.3315 0.1759 0
0.07 0 0.1574 0.2981 0.4082 0.4778 0.5015 0.4778 0.4082 0.2981 0.1574 0
0.08 0 0.1419 0.2693 0.3698 0.4338 0.4558 0.4338 0.3698 0.2697 0.1419 0
0.09 0 0.183 0.2437 0.3351 0.3936 0.4137 0.3936 0.3351 0.2437 0.1283 0
0.1 0 0.1161 0.2208 0.3038 0.3570 0.3753 0.3570 0.3038 0.2208 0.1161 0

Величины, полученные методом Кранка-Николсона, достаточно близки к

аналитическому решению u(x,t) = sin(πx)e-π2 t + sin(3πx)e-9π2 t , истинные значения для последнего представлены в таблице 2

Максимальная погрешность для данных параметров равна 0,005

Таблица 2 – точные значения u(х i , ti ), при t=0.1

xi 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
t11
0.1 0 0.1153 0.2192 0.3016 0.3544 0.3726 0.3544 0.3016 0.2192 0.1153 0

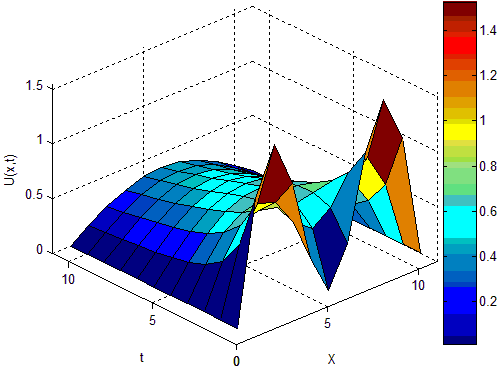
Рисунок 5 –Решениеu= u(х i , ti ), для метода Кранка-Николсона


ЗАКЛЮЧЕНИЕ

В зависимости от формы области, краевых условий, коэффициентов исходного уравнения метод конечных разностей имеет погрешности аппроксимации от первого до четвертого порядка относительно шага. В силу этого они успешно используются для разработки программных комплексов автоматизированного проектирования технических объектов.

В МКР строятся, как правило, регулярные сетки, особенности геометрии области учитываются только в около граничных узлах. В связи с этим МКР чаще применяется для анализа задач с прямолинейными границами областей определения функций.

Проблемой методов конечных разностей является высокая размерность результирующей системы алгебраических уравнений (несколько десятков тысяч в реальных задачах. Поэтому реализация методов конечных разностей в составе САПР требует разработки специальных способов хранения матрицы коэффициентов системы и методов решения последней.


Библиографический список

1 Березин И.С., Жидков Н.П. Методы вычислений. Т.2. – М.: Физматгиз, 1962.

2 Мэтьюз, Джон, Г., Финк, Куртис, Д. Численные методы. Использование MATLAB, 3-е издание.— М. : Вильяме, 2001. — 720 с

3 Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1972.

4 Формалев В.Ф., Ревизников Д.Л. Численные методы. – М.: ФИЗМАТЛИТ, 2004. - 400 с.

5 Пирумов У.Г. Численные методы. – М.: Издательство МАИ, 1998.

6 Калиткин Н.Н. Численные методы. – М.: Наука, 1976.


ПРИЛОЖЕНИЕ А

Листинг программы для расчета по методу Кранка-Николсона

f.m

function F=f(x)

F=sin(pi*x)+sin(3*pi*x);

ft.m

К-во Просмотров: 374
Бесплатно скачать Контрольная работа: Конечно-разностный метод решения для уравнений параболического типа