Контрольная работа: Краткие сведения и задачи по курсу векторной и линейной алгебры

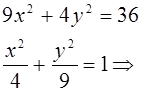
кривая второго порядка является эллипсом.

F₁ (c;0); F₂ (-c;0).

т.к.

Координаты центра: O’(-3,-1).

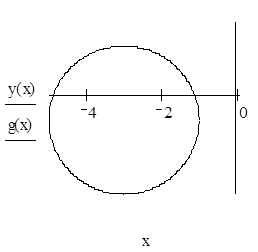
6. Преобразовать к полярным координатам уравнения линии.

1)

2)

Первое уравнение представляет собой (при любых значениях φ) полюс О. Второе – дает все точки линии, в том числе полюс. Поэтому первое уравнение можно отбросить. Следовательно, получаем:

Линейная алгебра

Матрицы

Ответы на вопросы

1. Дайте определение обратной матрицы. Какие вы знаете способы вычисления обратной матрицы?

Матрица В называется обратной для матрицы А, если выполняется условие АВ=ВА=Е, где Е – единичная матрица. Способы вычисления обратной матрицы: 1) использование алгебраических дополнений; 2) привести исходную матрицу к ступенчатому виду методом Гаусса, после чего необходимо преобразовать её в единичную .

2. Как записывается система уравнений в матрично-векторной форме? Как найти решение системы уравнений при помощи обратной матрицы?

Система уравнений в матрично-векторной форме записывается в виде: .

Решение системы уравнения при помощи обратной матрицы:

3. Сформулируйте, в чем состоит процедура Гаусса и для решения каких линейных задач применяется?

Процедура Гаусса используется для решения систем линейных уравнений и состоит в следующем:

Выполняются элементарные преобразования, вследствие чего можно получить два исхода: