Контрольная работа: Критерии оптимальности в эколого-математических моделях
.
Здесь значение СКО случайной величины 
может задаваться априорно, либо определяться экспериментально по выборке меньшего чем N объема.
Определение оценки дисперсии и ее среднего квадратического отклонения
Оценка дисперсии 
как экспериментальное значение второго центрального момента случайной величины X может быть вычислена по формуле
.
Так как значение 
априори неизвестно, то принимают
и тогда
. (13)
Математическое ожидание погрешности оценки равно
, (14)
что означает, что оценка (14) является смещенной.
Смещение пропорционально Dx и обратно пропорционально N. Это означает, что оценка Dx ,полученная согласно (14), - состоятельная.
Смещение устраняется с переходом к 
.
При этом вместо (13) имеем
. (15)
При больших значениях N результаты расчета по формулам (13)и (15)практически будут одинаковыми.
Выражение для дисперсии оценки (15), равной дисперсии погрешности
, при нормальном виде закона распределения X (для худшего случая) можно получить следующее [1-3]:
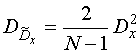. (16)
Зависимость среднего квадратического отклонения 
от его точного значения 
определяется выражением
.
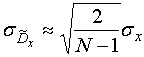3.3Определение корреляционного момента и коэффициента корреляции
Экспериментальное значение корреляционного момента Rxy как оценка смешанного центрального момента m 11 системы двух случайных величин равно
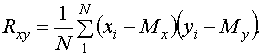
Так как значения Мх , Му неизвестны, то принимают 
, 
и тогда
ИЛИ
. (17)
Погрешность оценки 
(18)
Математическое ожидание погрешности (18)