Контрольная работа: Линейное программирование

3

3

30

1

10

1

70

2

50

4

1

20

5

3

v_j

5

3

4

2

Освободилось две клетки (1; 2) и (2; 1). Клетку (1; 2) считаем занятой с нулевой поставкой.

Среди оценок нет отрицательных, следовательно план перевозок Х₀ (таблица 1) оптимальный.

Исследуем этот план перевозок на оптимальность методом потенциалов. Потенциалы для занятых клеток удовлетворяют уравнениям: v_j = c_{ij +} u_i .

Пусть u₁ = 0; по клетке (1; 2) находим v₂ = 3; по клетке (1; 4) находим v₄ = 2; по клетке (2; 2) находим u₂ = -1; по клетке (3; 4) находим u₃ = 1; по клетке (3; 3) находим v₃ = 4; по клетке (4; 3) находим u₄ = 3; по клетке (4; 1) находим v₁ = 5.

Для всех клеток матрицы перевозок найдем оценки клеток d_ij = (u_i + c_ij ) - v_j :

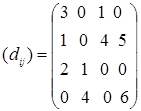
Так как среди оценок свободных клеток нет нулевых, то оптимальный план перевозок единственный.

Общие затраты на перевозки

F(X₁ ) = 2*50 + 4*40 + 3*30 + 1*10 + 2*50 + 1*20 = 480 ден. единиц

будут минимальными при: