Контрольная работа: Линейные функции

Получим уравнение плоскости:
![]()
Запишем условие перпендикулярности плоскостей:
![]()
Условие, что искомая плоскость:
через точку А: ![]() ;
;
через точку В: ![]() .
.
Получим систему уравнений:

Складываем 2-е и 3-е уравнения: ![]() , 1-е уравнение умножаем на 2 и вычитаем из полученного:
, 1-е уравнение умножаем на 2 и вычитаем из полученного:
![]()
Из 1-го уравнения: ![]() .
.
Из 3-го уравнения: ![]() . Принимаем
. Принимаем ![]() , получаем
, получаем
![]() .
.
Уравнение плоскости имеет вид:
![]()
№ 4. Найти расстояние от точки ![]() до прямой
до прямой ![]() .
.
Расстояние r найдем по формуле расстояния от точки ![]() до прямой, заданной уравнением в канонической форме:
до прямой, заданной уравнением в канонической форме:
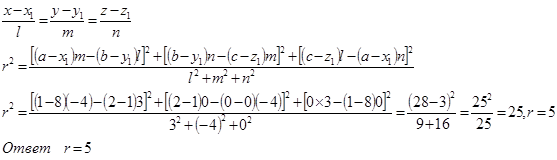
№ 5. Найти длину отрезка, отсекаемого от оси ординат плоскостью, которая проходит через точку ![]() перпендикулярно вектору
перпендикулярно вектору ![]() , где В — точка пересечения медиан треугольника, вершины которого совпадают с точками пересечения осей координат с плоскостью
, где В — точка пересечения медиан треугольника, вершины которого совпадают с точками пересечения осей координат с плоскостью
![]()
Для нахождения решения найдем уравнение плоскости, которая проходит через точку А в заданном направлении и подставим в это уравнение значение ![]() .
.
Для этого вначале найдем координаты точки В.
Точку пересечения заданной плоскости с осью ОХ найдем из уравнения:
![]()
с осью OY:
![]()
с осью OZ: