Контрольная работа: Линейные функции

Получим треугольник с вершинами: .

Найдем координаты середины стороны по формуле:

.

— середина стороны .

Теперь найдем точку В, используя свойство: медианы треугольника делятся в точке пересечения в отношении 2:1, считая от вершины. Используем формулу:

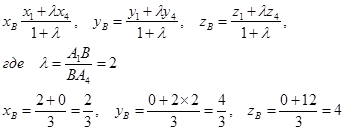
Точка пересечения медиан имеет координаты .

Найдем координаты вектора .

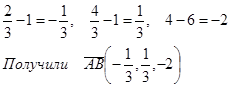
Уравнение искомой плоскости, проходящей через точку перпендикулярно вектору имеет вид:

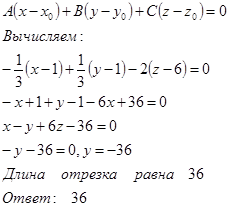
№ 6. Две прямые параллельны плоскости . Первая прямая проходит через точку и пересекает ось абсцисс, вторая — через точку и пересекает ось ординат. Найти косинус острого угла между направляющими векторами этих прямых.

Для нахождения направляющих векторов прямых используем условие параллельности прямой и плоскости

и условие, что прямая проходит через ось абсцисс, т.е. выполняется соотношение в точке (x,0,0).

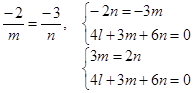
подставляем из 1-го уравнения во второе, получим

Полагаем тогда .

Получили направляющий вектор первой прямой (6,-2,-3).

Аналогично для второй прямой (она проходит через точку (0,y,0)

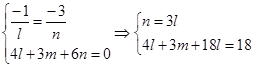
Из второго уравнения

Косинус найдем по формуле:

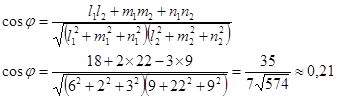
№ 7. Найти координаты центра окружности радиусом 5, касающейся прямой в точке М (2,0), если известно, что точка С расположена в первой четверти.

Переформулируем задачу:

Найти точку, лежащую на прямой, перпендикулярной прямой , проходящей через точку М (2,0) и отстоящую от нее на 5 ед.