Контрольная работа: Линейные функции
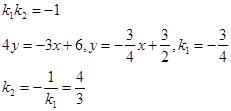
Получаем уравнение прямой
![]()
Используем формулу расстояния между двумя точками:
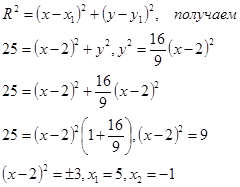
По условию второе решение не походит, т.к. x<0.
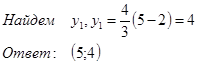
№ 8. Дана кривая ![]()
8.1. Доказать, что эта кривая — гипербола.
![]() — это каноническое уравнение гиперболы. Приведем исходное уравнение к этому виду
— это каноническое уравнение гиперболы. Приведем исходное уравнение к этому виду
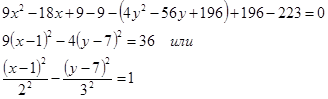
Это каноническое уравнение гиперболы.
8.2 Найти координаты ее центра симметрии.
Сделаем схематический чертеж:
Центр симметрии гиперболы в точке ![]() .
.
![]() .
.
8.3. Найти действительную и мнимую полуоси.
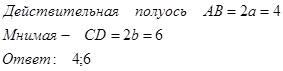
8.4. Записать уравнение фокальной оси.
Фокальная ось проходит через фокус ![]() , р-фокальный параметр (половина хорды, проведенной через фокус перпендикулярно действительной оси).
, р-фокальный параметр (половина хорды, проведенной через фокус перпендикулярно действительной оси).
Уравнение ![]() , где
, где
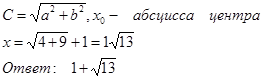
8.5. Построить данную гиперболу построение проведено в п.8.2.
№ 9. Дана кривая ![]() .
.
9.1. Доказать, что данная кривая — парабола.
Каноническое уравнение параболы ![]() , заданное уравнение приведем к этому виду
, заданное уравнение приведем к этому виду
![]()
следовательно, имеем параболу.
9.2. Найти координаты ее вершины.