Контрольная работа: Математическая статистика

п = 90 + 690 + 220 = 1000 ,

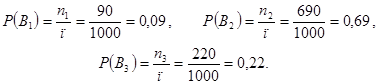
Найдем вероятности события А при условии, что события B_i ( i = 1,2,3 ) наступили, т.е. найдем вероятности выбора бракованной лампы при условии, что лампы взяты из 1-ой, 2-ой, 3-ей партий :

По формуле полной вероятности найдем искомую вероятность:

Задание 9. В магазин поступают однотипные изделия с трех заводов, причем i-й завод поставляет т_i % изделий ( i = 1, 2, 3). Среди изделий i-го завода n_i % первосортных. Куплено одно изделие. Оно оказалось первосортным. Определить вероятность того, что купленное изделие выпущено j-ым заводом.

.

Решение:

Определимся с событиями:

А – купленное изделие первосортное;

изделие выпущено i-ым заводом, .

Запишем вероятности событий В_i :

Запишем условные вероятности, т.е. вероятности того, что купленное изделие первосортное при условии, что оно выпущено i-ым заводом:

Вероятность того, что купленное первосортное изделие выпущено 1-ым заводом, вычислим по формуле Бейеса:

Задание 10. Вероятность наступления некоторого события в каждом из 100 независимых испытаний равна р = 0,8. Определить вероятность того, что число т наступлений события удовлетворяет следующему неравенству:

k₁ = 75;

k₂ = 90

Решение:

Воспользуемся интегральной теоремой Лапласа :

где Ф(х) – функция Лапласа,

Найдем х₁ и х₂ :