Контрольная работа: Математическая статистика

Учитывая, что функция Лапласа нечетная, т.е. , получим

.

По таблице найдем :

Искомая вероятность

Задание 12. Дискретная случайная величина Х принимает только два значения х₁ и х₂ , причем . Известна вероятность р₁ = 0,7 возможного значения х₁ , математическое ожидание М(Х ) = 1,3 и дисперсия D(X ) = 0,21. Найти закон распределения этой случайной величины.

Решение:

Сумма вероятностей всех возможных значений ДСВ равна 1. Отсюда вероятность того, что Х примет значение х₂ равна

р₂ = 1 – р₁ = 1 – 0,7 = 0,3.

Запишем закон распределения ДСВ Х :

Х	х1	х2
р	0,7	0,3

Для нахождения значений х₁ и х₂ составим систему уравнений и решим ее:

или ;

или

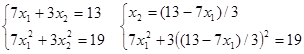
7x₁ ² + =19 (x 3)

70x₁ ² -182x₁ +112 = 0

По условию задачи . Следовательно, задаче удовлетворяет только решение , и искомый закон распределения будет иметь вид:

Х	1	2
р	0,7	0,3

Задание 12. Непрерывная случайная величина задана функцией распределения . Требуется найти:

а) функцию плотности распределения ;

б) математическое ожидание ;

в) дисперсию ;

г) среднее квадратическое отклонение .

Построить графики функций и .