Контрольная работа: Математические методы оптимизации

Для определения целевой функции двойственной задачи двойственные переменные и умножаются на правые части равенств и складываются:

.

Каждой переменной прямой задачи соответствует ограничение двойственной задачи. Левые части этих ограничений для переменной записываются следующим образом. Двойственные переменные и умножаются на коэффициенты перед переменной и складываются: .

Аналогично, записываются левые части ограничений для переменной . Двойственные переменные и умножаются на коэффициенты перед переменной и складываются: . Левая часть ограничений для переменной равна , а для переменной . Правые части ограничений равны коэффициентам 30, 25, 0, 0 целевой функции

перед переменными . Левые и правые части ограничений соединяются знаком .

В результате двойственная задача имеет вид:

найти двойственные переменные и , при которых целевая функция минимальна

при ограничениях

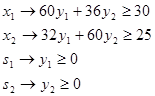
Переменные , называются допустимым решением двойственной задачи, если они удовлетворяют всем ограничениям и оптимальными, если они допустимые и на них целевая функция достигает минимума.

Экономический смысл двойственной задачи:

двойственная переменная определяет теневую цену работы 1 минуты оборудования линии 1, а двойственная переменная определяет теневую цену работы 1 минуты оборудования линии 2.

Тогда целевая функция задаёт стоимость времени работы оборудования в теневых ценах соответственно для линии 1 и линии 2.

Выражение определяет стоимость 60 минут и 36 минут, затраченных на изготовление единицы изделия А в теневых ценах, а выражение определяет стоимость 32 минут и 60 минут, затраченных на изготовление единицы изделия В в теневых ценах.

Определим величины приведённых стоимостей.

Если величина положительна, то стоимость ресурсов больше рыночной цены этого продукта. В этом случае производство продукта убыточно. Если величина отрицательна, то стоимость ресурсов меньше рыночной цены этого продукта. Если величина равна 0, то стоимость ресурсов равна рыночной цене. Ограничения двойственной задачи

Отсюда следует, что при допустимых теневых ценах производство обоих продуктов неприбыльно.

Можно дать следующую экономическую интерпретацию двойственной задачи. Некоторая фирма предлагает производителю продукции продать ей все запасы ресурсов по теневым ценам и . Решение двойственной задачи определяет минимальный уровень рыночных цен , при котором производить продукцию неприбыльно.

Найдём оптимальное решение двойственной задачи

Из первого задания следует, что допустимое базисное решение

является оптимальным решением прямой задачи.

По оптимальному базисному решению прямой задачи найдём оптимальное решение двойственной. Для этого все ограничения двойственной задачи, соответствующие базисным переменным нужно заменить равенствами

Из этих равенств найдём оптимальные значения двойственных переменных , минимальное значение целевой функции равно