Контрольная работа: Математические методы оптимизации

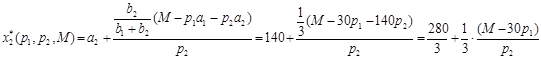
Эти формулы определяют спрос на продукцию при любых ценах и доходах.

3. Оценим влияние на спрос изменения дохода обоих товаров. Найдём реакцию спроса на изменение дохода на 1 денежную единицу. Частные производные по доходу 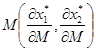показывают изменение спроса на первый и второй товары соответственно при возрастании дохода на 1 денежную единицу.

Дифференцируя полученные выше функции спроса по М, получаем

.

Вычислим эти частные производные при заданных и :

.

Так как значения частных производных положительные, то оба товара являются ценными: с ростом дохода на 1 денежную единицу спрос на оба товара растёт: спрос на первый товар увеличивается на , а второго - на .

При увеличении дохода потребителя на 30 денежных единиц спрос на первый товар увеличится на единицы, а второго на и составит

, .

При уменьшении дохода потребителя на 60 денежных единиц спрос на первый товар снизится на единиц, а спрос на второй товар снизится на единиц и составит соответственно:

, .