Контрольная работа: Математические основы теории систем
Связный ориентированный граф G (Х , Г) задан множеством вершин X ={ x 1 , x 2 ,…,xn } и отображением Г xi ={ x | I ± k | ,x | I ± l | } ,i =1 , 2 ,… ,n . Здесь i - текущий номер вершины, n- количество вершин графа. Значение индексов n , k и l возьмем из табл.1 в соответствии с номером варианта. Индексы k и l формируют значения индексов a ,b , g … переменной x в отображении Г xi = { x a ,x b ,x g ,…} . Если значения индексов a , b ,g … переменной x не соответствуют ни одному из номеров вершин графа, то эта переменная не учитывается во множестве Г xi .
Выполнить следующие действия:
а) определить исходный граф и ассоциированный с ним неориентированный граф графическим, матричным и аналитическим способами;
б) установить центры и периферийные вершины графов, найти радиусы и диаметры графов;
в) выделить в ориентированном графе два подграфа. Найти объединение, пересечение и разность подграфов;
г) описать систему уравнений, соответствующую сигнальному графу, считая, что передача между вершинами xi и xj
![]() i*j при i ³ j ;
i*j при i ³ j ;
Kij =
1/ ( p +1) при i < j .
Найти передачу между вершинами x 1 и xn , используя правило Мезона. Построить структуру кибернетической системы, определяемой топологией графа;
Таблица 1
|
№ варианта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| N | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 6 | 6 | 6 |
| K | 2 | 3 | 4 | 1 | 1 | 1 | 3 | 5 | 2 | 4 | 2 | 3 | 4 | 5 | 6 |
| L | 1 | 1 | 1 | 2 | 3 | 4 | 2 | 1 | 3 | 3 | 1 | 1 | 1 | 1 | 1 |
|
№ варианта | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| N | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 7 | 7 | 7 | 7 | 7 | 7 |
| K | 1 | 1 | 1 | 1 | 3 | 2 | 5 | 5 | 2 | 3 | 4 | 5 | 6 | 5 | 3 |
| L | 2 | 3 | 4 | 5 | 2 | 3 | 2 | 3 | 3 | 2 | 3 | 2 | 1 | 3 | 5 |
Решение:
Множество вершин
X = { x 1 , x 2 ,x 3 , x 4 , x 5 , x 6 }, n = 6 k = 2, l = 1 Г xi ={ x | I ± k | ,x | I ± l | }.
а) определим исходный граф и ассоциированный с ним неориентированный граф графическим, матричным и аналитическим способами:
Определим граф аналитическим способом:
Г x 1 = { x 1 , x 3 , x 2 };
Г x 2 = { x 4 , x 1 , x 3 };
Г x 3 = { x 1 , x 5 , x 2 , x 4 };
Г x 4 = { x 2 , x 6 , x 3 , x 5 };
Г x 5 = { x3 , x 4 , x 6 };
Г x 6 = { x4 ,x 5 }.
Ориентированный граф графическим способом:
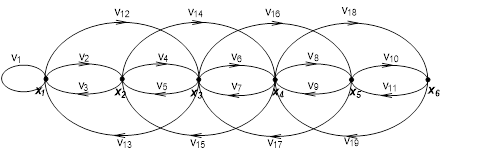
Неориентированный граф графическим способом:
--> ЧИТАТЬ ПОЛНОСТЬЮ <--