Контрольная работа: Математические основы теории систем
Матрица D = D + - D - называется матрицей инцидентности сети Петри,

2. При начальной маркировке μ0 [1 3 0 1 2] сети Петри разрешенными являются переходы t 1 и t 2 .
Условия срабатывания для перехода t 3 и t 4 не выполняется.
Переход t 1
[μ0 ] ≥ [1000]*D - = [1000] ·  ; [1 3 0 1 2] ≥ [00001] –
; [1 3 0 1 2] ≥ [00001] –
условие выполняется, переход разрешен.
Новая маркировка при срабатывании перехода t 1 равна:

![]() .
.
Переход t 2
[μ0 ] ≥ [0100]* D - = [0100]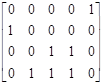 ·; [1 3 0 1 2] ≥ [10000] –
·; [1 3 0 1 2] ≥ [10000] –
условие выполняется, переход разрешен.
Новая маркировка при срабатывании перехода t 2 равна:
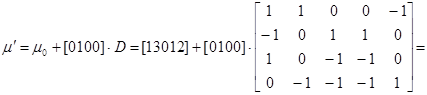
![]() .
.
Переход t 3
[μ0 ] ≥ [0010]* D - = [0010]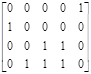 ·; [1 3 0 1 2] ≥ [00110] - условие не
·; [1 3 0 1 2] ≥ [00110] - условие не
выполняется, переход запрещен.
Переход t 4
[μ0 ] ≥ [0001]* D - = [0001]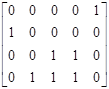 ·; [1 3 0 1 2] ≥ [01110] –
·; [1 3 0 1 2] ≥ [01110] –
условие не выполняется, переход запрещен.
Построим дерево достижимости заданной сети.
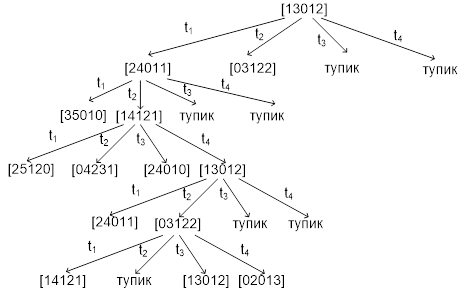
Проверим, является ли достижимой одна из маркировок, полученных на пятом шаге построения дерева, составив и решив матричные уравнения.
Уравнение ![]() принимает вид
принимает вид
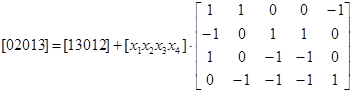
Перенесем ![]() в левую часть и выполним умножение, тогда
в левую часть и выполним умножение, тогда
![]() .
.